3D Geometry 1 Question 3
The vertices $B$ and $C$ of a $\triangle A B C$ lie on the line, $\frac{x+2}{3}=\frac{y-1}{0}=\frac{z}{4}$ such that $B C=5$ units. Then, the area (in sq units) of this triangle, given that the point $A(1,-1,2)$ is
(2019 Main, 9 April II)
(a) $\sqrt{34}$
(b) $2 \sqrt{34}$
(c) $5 \sqrt{17}$
(d) 6
Show Answer
Answer:
Correct Answer: (a)
Solution:
Method 1:
Let’s approach this step-by-step:
-
First, we need to find the coordinates of points B and C. We know they lie on the line given by the equation:
$\frac{x+2}{3} = \frac{y-1}{0} = \frac{z}{4}$
-
This line passes through the point (-2, 1, 0) and is parallel to the vector (3, 0, 4). So we can parameterize the line as:
$B(-2 + 3t, 1, 4t)$ and $C(-2 + 3s, 1, 4s)$, where $t$ and $s$ are real numbers.
-
Now, we’re told that the distance between B and C is 5 units. Using the distance formula in 3D, we get:
$\sqrt{(3s - 3t)^2 + (4s - 4t)^2} = 5$
$\sqrt{9(s - t)^2 + 16(s - t)^2} = 5$
$5|s - t| = 5$
$|s - t| = 1$
-
Without loss of generality, let’s choose $t = 0$ and $s = 1$. Then the coordinates of B and C are:
$B(-2, 1, 0)$ and $C(1, 1, 4)$
-
Now we have the coordinates of all three vertices of the triangle:
$A(1, -1, 2)$, $B(-2, 1, 0)$, and $C(1, 1, 4)$
-
To find the area of the triangle, we can use the formula:
$Area = \frac{1}{2}||(B - A) \times (C - A)||$
where $\times$ denotes the cross product and $||$ denotes the magnitude of a vector.
-
$B - A = (-3, 2, -2)$ and $C - A = (0, 2, 2)$
$(B - A) \times (C - A) = (-8, -6, 6)$
$||(B - A) \times (C - A)|| = \sqrt{(-8)^2 + (-6)^2 + 6^2} = \sqrt{136} = 2\sqrt{34}$
-
Therefore, the area of the triangle is:
$Area = \frac{1}{2} \cdot 2\sqrt{34} = \sqrt{34}$ square units.
So the correct answer is (a) $\sqrt{34}$ square units[1].
Alternate Method
Given line is $\frac{x+2}{3}=\frac{y-1}{0}=\frac{z}{4}$
Vector along line is, $\mathbf{a}=3 \hat{\mathbf{i}}+4 \hat{\mathbf{k}}$
and vector joining the points $(1,-1,2)$ to $(-2,1,0)$ is $\mathbf{b}=(1+2) \hat{\mathbf{i}}+(-1-1) \hat{\mathbf{j}}+(2-0) \hat{\mathbf{k}}$
$ =3 \hat{\mathbf{j}}-2 \hat{\mathbf{j}}+2 \hat{\mathbf{k}} $
and $|\mathbf{B C}|=5$ units
Now, area of required $\triangle A B C$
$ =\frac{1}{2}|\mathbf{B C}||\mathbf{b}||\sin \theta| $
[where $\theta$ is angle between vectors $\mathbf{a}$ and $\mathbf{b}$ ]
$\because|\mathbf{b}| \sin \theta=\frac{|\mathbf{a} \times \mathbf{b}|}{|\mathbf{a}|}$,
$ \because \quad|\mathbf{a} \times \mathbf{b}|=\left|\begin{array}{ccc} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 3 & 0 & 4 \\ 3 & -2 & 2 \end{array}\right|=8 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}-6 \hat{\mathbf{k}} $
$\Rightarrow \quad|\mathbf{a} \times \mathbf{b}|=\sqrt{64+36+36}$
$ =\sqrt{136}=2 \sqrt{34} $
and $\quad|\mathbf{a}|=\sqrt{9+16}=5$
$\therefore \quad|\mathbf{b}| \sin \theta=\frac{2 \sqrt{34}}{5}$
On substituting these values in Eq. (i), we get
Required area $=\frac{1}{2} \times 5 \times \frac{2 \sqrt{34}}{5}=\sqrt{34}$ sq units
Alternate Method
Given line is $\frac{x+2}{3}=\frac{y-1}{0}=\frac{z}{4}=\lambda$ (let)
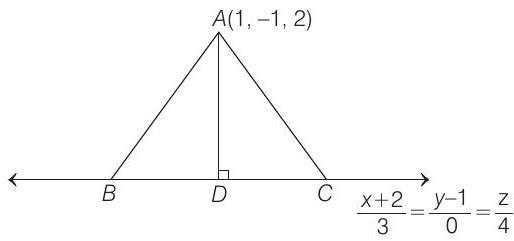
Since, point $D$ lies on the line $B C$.
$\therefore$ Coordinates of $D=(3 \lambda-2,1,4 \lambda)$
Now, $\quad D R$ of $B C \Rightarrow a _1=3, b _1=0, c _1=4$
and $D R$ of $A D \Rightarrow a _2=3 \lambda-3, b _2=2, c _2=4 \lambda-2$
Since, $\quad A D \perp B C, a _1 a _2+b _1 b _2+c _1 c _2=0$
$ 3 \times(3 \lambda-3)+0(2)+4(4 \lambda-2)=0 $
$\Rightarrow \quad 9 \lambda-9+0+16 \lambda-8=0$
$\Rightarrow \quad 25 \lambda-17=0$ $\Rightarrow \quad \lambda=\frac{17}{25}$
$\therefore$ Coordinates of $D=\frac{1}{25}, 1, \frac{68}{25}$.
Now, $\quad A D=\sqrt{1-\frac{1}{25}^{2}+(-1-1)^{2}+2-\frac{68}{25}^{2}}$
$=\sqrt{\frac{24}{25}^{2}+(-2)^{2}+\frac{-18}{25}^{2}}$
$=\sqrt{\frac{576}{625}+4+\frac{324}{625}}=\frac{2}{5} \sqrt{34}$
$\therefore$ Area of $\triangle A B C=\frac{1}{2} B C \times A D$
$ \begin{aligned} & =\frac{1}{2} \times 5 \times \frac{2}{5} \sqrt{34} \\ & =\sqrt{34} \text { sq units } \end{aligned} $
