3D Geometry 3 Question 48
48. A variable plane
(2005, 2M)
(a) 9
(b) 3
(c)
(d)
Show Answer
Answer:
Correct Answer: 48. (d)
Solution:
- Since,
And its distance from origin
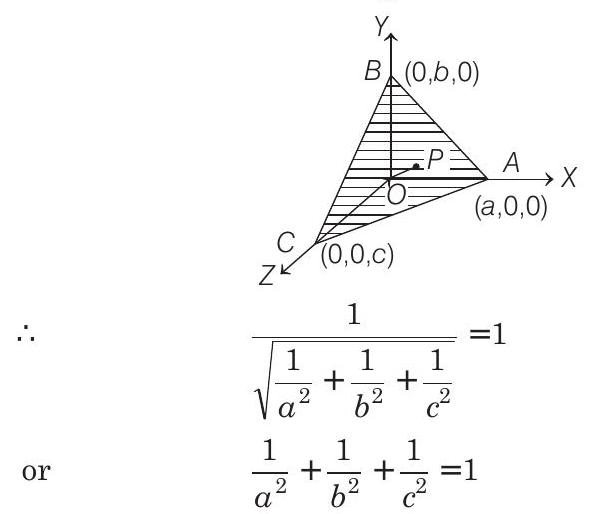
where,
From Eqs. (i) and (ii),






