3D Geometry 3 Question 43
43. If the distance of the point $P(1,-2,1)$ from the plane $x+2 y-2 z=\alpha$, where $\alpha>0$, is 5 , then the foot of the perpendicular form $P$ to the plane is
(2010)
(a) $\frac{8}{3}, \frac{4}{3},-\frac{7}{3}$
(b) $\frac{4}{3}, \frac{4}{3}, \frac{1}{3}$
(c) $\frac{1}{3}, \frac{2}{3}, \frac{10}{3}$
(d) $\frac{2}{3}, \frac{1}{3}, \frac{5}{2}$
Show Answer
Answer:
Correct Answer: 43. (a)
Solution:
- Distance of point $P$ from plane $=5$
$ \begin{array}{ll} \therefore & 5=\left|\frac{1-4-2-\alpha}{3}\right| \\ \Rightarrow & \alpha=10 \end{array} $
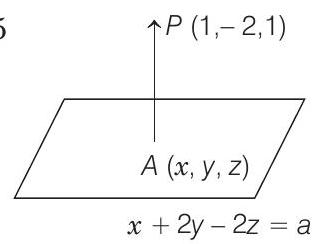
Foot of perpendicular
$ \begin{aligned} \frac{x-1}{1} & =\frac{y+2}{2}=\frac{z-1}{-2}=\frac{5}{3} \\ \Rightarrow \quad x & =\frac{8}{3}, y=\frac{4}{3}, z=-\frac{7}{3} \end{aligned} $
Thus, the foot of the perpendicular is $A \frac{8}{3}, \frac{4}{3},-\frac{7}{3}$.
