3D Geometry 3 Question 42
42. The point $P$ is the intersection of the straight line joining the points $Q(2,3,5)$ and $R(1,-1,4)$ with the plane $5 x-4 y-z=1$. If $S$ is the foot of the perpendicular drawn from the point $T(2,1,4)$ to $Q R$, then the length of the line segment $P S$ is
(2012)
(a) $\frac{1}{\sqrt{2}}$
(b) $\sqrt{2}$
(c) 2
(d) $2 \sqrt{2}$
Show Answer
Answer:
Correct Answer: 42. (a)
Solution:
- PLAN It is based on two concepts one is intersection of straight line and plane and other is the foot of perpendicular from a point to the straight line.
Description of Situation
(i) If the straight line
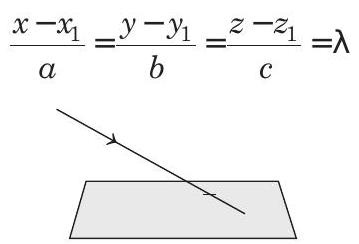
intersects the plane $A x+B y+C z+d=0$.
Then, $\left(a \lambda+x _1, b \lambda+y _1, c \lambda+z _1\right)$ would satisfy
$ A x+B y+C z+d=0 $
(ii) If $A$ is the foot of perpendicular from $P$ to $l$.
Then, (DR’s of $P A$ ) is perpendicular to DR’s of $l$.
$ \Rightarrow \quad \overline{P A} \cdot \bar{l}=0 $
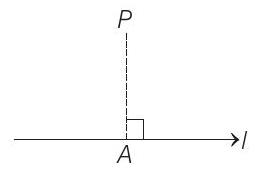
Equation of straight line $Q R$, is
$ \begin{aligned} & \frac{x-2}{1-2}=\frac{y-3}{-1-3}=\frac{z-5}{4-5} \\ & \Rightarrow \quad \frac{x-2}{-1}=\frac{y-3}{-4}=\frac{z-5}{-1} \\ & \Rightarrow \quad \frac{x-2}{1}=\frac{y-3}{4}=\frac{z-5}{1}=\lambda \\ & \therefore P(\lambda+2,4 \lambda+3, \lambda+5) \text { must lie on } 5 x-4 y-z=1 \text {. } \\ & \Rightarrow \quad 5(\lambda+2)-4(4 \lambda+3)-(\lambda+5)=1 \\ & \Rightarrow \quad 5 \lambda+10-16 \lambda-12-\lambda-5=1 \\ & \Rightarrow \quad-7-12 \lambda=1 \\ & \therefore \quad \lambda=\frac{-2}{3} \\ & \text { or } \\ & P \frac{4}{3}, \frac{1}{3}, \frac{13}{3} \end{aligned} $
Again, we can assume $S$ from Eq.(i),
$ \text { as } S(\mu+2,4 \mu+3, \mu+5) $
$\therefore \quad$ DR’s of $T S=<\mu+2-2,4 \mu+3-1, \mu+5-4>$
$ =<\mu, 4 \mu+2, \mu+1> $
and DR’s of $Q R=<1,4,1>$
Since, perpendicular
$\therefore \quad 1(\mu)+4(4 \mu+2)+1(\mu+1)=0$
$\Rightarrow \mu=-\frac{1}{2}$ and $S \frac{3}{2}, 1, \frac{9}{2}$
$\therefore$ Length of $P S=\sqrt{\frac{3}{2}-\frac{4}{3}^{2}+1-\frac{1}{3}^{2}+\frac{9}{2}-\frac{13}{3}^{2}}=\frac{1}{\sqrt{2}}$
