Thermodynamics and Thermochemistry - Result Question 91
####16. An ideal gas undergoes isothermal compression from $5 m^{3}$ to $1 m^{3}$ against a constant external pressure of $4 Nm^{-2}$. Heat released in this process is used to increase the temperature of 1 mole of Al. If molar heat capacity of $Al$ is $24 J mol^{-1} K^{-1}$, the temperature of $Al$ increases by
(2019 Main, 10 Jan II)
(a) $\frac{3}{2} K$
(b) $1 K$
(c) $2 K$
(d) $\frac{2}{3} K$
17 A process has $\Delta H=200 J mol^{-1}$ and $\Delta S=40 JK^{-1} mol^{-1}$. Out of the values given below, choose the minimum temperature above which the process will be spontaneous
(2019 Main, 10 Jan I)
(a) $20 K$
(b) $4 K$
(c) $5 K$
(d) $12 K$
18 The entropy change associated with the conversion of $1 kg$ of ice at $273 K$ to water vapours at $383 K$ is
(Specific heat of water liquid and water vapour are $4.2 kJ$ $K^{-1} kg^{-1}$ and $2.0 kJK^{-1} kg^{-1}$; heat of liquid fusion and vapourisation of water are $334 kJ kg^{-1}$ and $2491 kJkg^{-1}$ respectively $). \quad(\log 273=2.436, \quad \log 373=2.572$, $\log 383=2.583)$
(2019 Main, 9 Jan II)
(a) $9.26 kJ kg^{-1} K^{-1}$
(b) $8.49 kJ kg^{-1} K^{-1}$
(c) $7.90 kJ kg^{-1} K^{-1}$
(d) $2.64 kJ kg^{-1} K^{-1}$
19 Consider the reversible isothermal expansion of an ideal gas in a closed system at two different temperatures $T _1$ and $T _2$ $\left(T _1<T _2\right)$. The correct graphical depiction of the dependence of work done $(W)$ on the final volume $(V)$ is
(2019 Main, 9 Jan I)
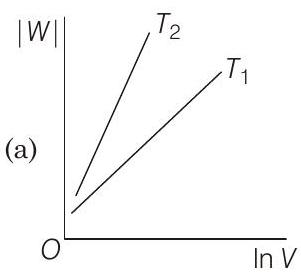
(b)
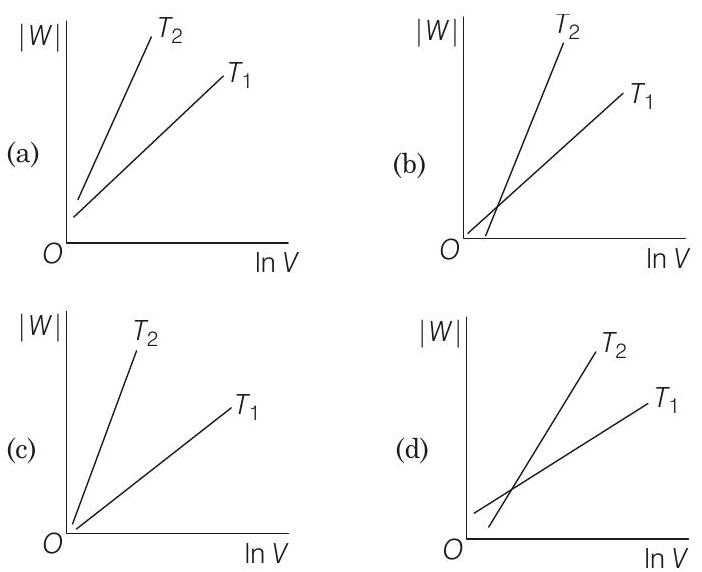
(d)
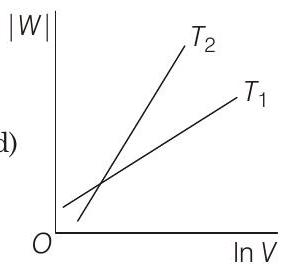
Show Answer
Solution:
- It is an irreversible isothermal compression of an ideal gas.
(i) $d E=d q+p\left(V _f-V _i\right)$
where, $d E=$ Internal energy change
$$ \begin{aligned} d q & =\text { amount of heat released } \ \Rightarrow \quad 0 & =d q+p\left(V _f-V _i\right) \end{aligned} $$
$[\because d E=0$ for an isothermal process $]$
$\Rightarrow d q=-4(1-5)=16 J$
(ii) $\quad d q=n \times C \times \Delta T$ (for $Al$ )
$\Rightarrow 16 J=1 mol \times 24 J mol^{-1} K^{-1} \times \Delta T$
$\Rightarrow \Delta T=\frac{16}{24} K=\frac{2}{3} K$






