Thermodynamics and Thermochemistry - Result Question 42
####42. An ideal gas in thermally insulated vessel at internal pressure $=p _1$, volume $=V _1$ and absolute temperature $=T _1$ expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are $p _2, V _2$ and $T _2$, respectively. For this expansion
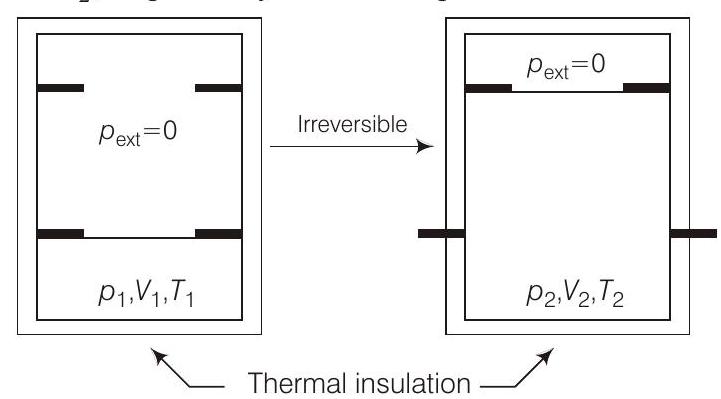
(a) $q=0$
(b) $T _2=T _1$
(c) $p _2 V _2=p _1 V _1$
(d) $p _2 V _2^{\gamma}=p _1 V _1^{\gamma}$
(2014 Adv.)
Show Answer
Solution:
- PLAN This problem includes concept of isothermal adiabatic irreversible expansion.
Process is adiabatic because of the use of thermal insolution therefore, $q=0$
$$ \because \quad p _{\text {ext }}=0 $$
$$ w=p _{ext} \cdot \Delta V=0 \times \Delta V=0 $$
Internal energy can be written as
$$ \Delta U=q+W=0 $$
The change in internal energy of an ideal gas depends only on temperature and change in internal energy $(\Delta U)=0$ therefore, $\Delta T=0$ hence, process is isothermal and
and
$$ \begin{gathered} T _2=T _1 \ p _2 V _2=p _1 V _1 \end{gathered} $$
(d) $p _2 V _2^{\gamma}=p _1 V _1^{\gamma}$ is incorrect, it is valid for adiabatic reversible process.
Hence, only (a), (b) and (c) are correct choices.






