States of Matter - Result Question 1
####1. Points I, II and III in the following plot respectively correspond to ( $v _{mp}:$ most probable velocity)
(2019 Main, 10 April II)
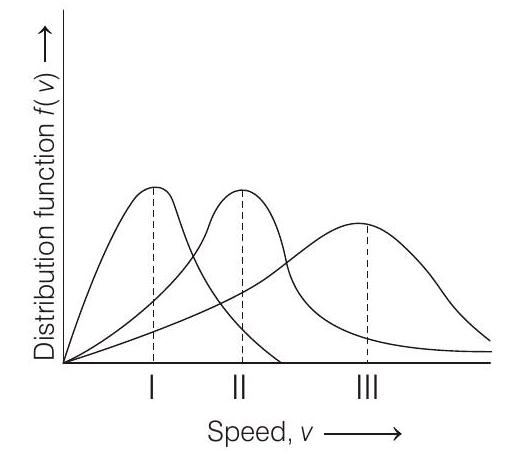
(a) $v _{mp}$ of $H _2(300 K)$; $v _{mp}$ of $N _2(300 K)$; $v _{mp}$ of $O _2(400 K)$
(b) $v _{mp}$ of $O _2(400 K) ; v _{mp}$ of $N _2(300 K) ; v _{mp}$ of $H _2(300 K)$
(c) $v _{mp}$ of $N _2(300 K)$; $v _{mp}$ of $O _2(400 K)$; $v _{mp}$ of $H _2(300 K)$
(d) $v _{mp}$ of $N _2(300 K) ; v _{mp}$ of $H _2(300 K) ; v _{mp}$ of $O _2(400 K)$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
Key Idea From kinetic gas equation,
Most probable velocity $\left(v _{mp}\right)=\sqrt{\frac{2 R T}{M}}$
where, $R=$ gas constant, $T=$ temperature, $M=$ molecular mass
| $v _{mp}=\sqrt{\frac{2 R T}{M}}$, i.e. $v _{mp} \propto \sqrt{\frac{T}{M}}$ | |||
|---|---|---|---|
| Gas | $\boldsymbol{M}$ | $\boldsymbol{T}(K)$ | $\sqrt{\boldsymbol{T} / \boldsymbol{M}}$ |
| $H _2$ | 2 | 300 | $\sqrt{300 / 2}=\sqrt{150} \ldots$ III (Highest) |
| $N _2$ | 28 | 300 | $\sqrt{300 / 28}=\sqrt{10.71} \ldots$ I (Lowest) |
| $O _2$ | 32 | 400 | $\sqrt{400 / 32}=\sqrt{12.5} \ldots$ II |
So,
I. corresponds to $v _{mp}$ of $N _2(300 K)$
II. corresponds to $v _{mp}$ of $O _2(400 K)$
III. corresponds to $v _{mp}$ of $H _2(300 K)$






