Solutions and Colligative Properties - Result Question 33
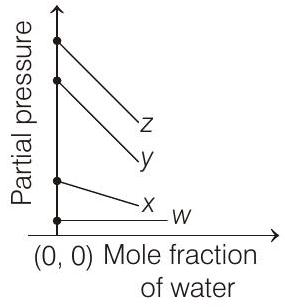
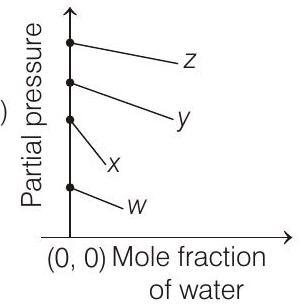
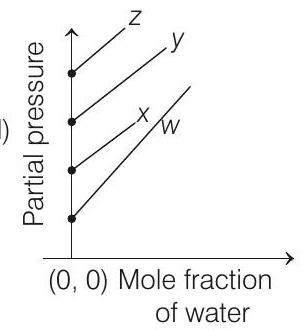
####4. For the solution of the gases $w, x, y$ and $z$ in water at $298 K$, the Henry’s law constants $\left(K _H\right)$ are $0.5,2,35$ and $40 K$ bar, respectively. The correct plot for the given data is
(2019 Main, 8 April II) (a)
(c)
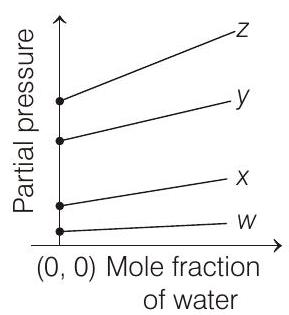
(b)
(d)
Show Answer
Solution:
- According to Henry’s law (at constant temperature)
$p _{\text {gas }}=K _H \times \chi _{\text {gas (solute) }}=K _H \times\left[1-\chi _{H _2 O \text { (solvent) }}\right]$
$p _{\text {gas }}=K _H-K _H \chi _{H _2 O}$ $p _{\text {gas }}=$ partial pressure of the gas above its solution with a liquid (solvent) say water.
$\chi _{\text {gas }}=$ mole fraction of the gas (solute) in the solution.
$\chi _{H _2 O}=$ mole fraction of water (solvent).
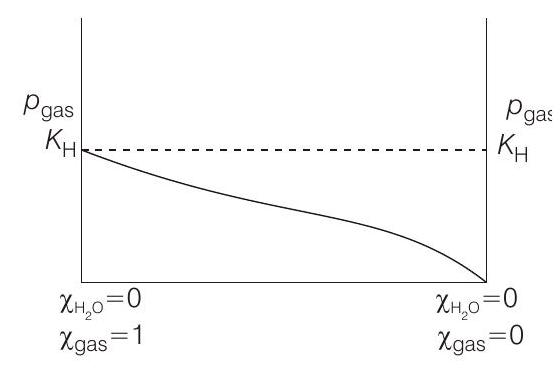
[i.e. $p _{\text {gas }}=K _H$ ] Higher the value of $K _H$, higher
will be the partial pressure of the gas $\left(p _{\text {gas }}\right)$, at a given temperature. The plot of $p _{\text {gas }} v s \chi _{H _2 O}$ gives a (-ve) slope.
$$ p _{\text {gas }}=K _H-K _H \times \chi _{H _2 O} $$
Comparing the above equation with the equation of straight line $y=m x+c$
Slope $=-K _H$, intercept $=K _H$
So, (i) Higher the value of $K _H$, more (-ve) will be the slope and it is for $z\left(K _H=40 K\right.$ bar $)$
(ii) Higher the value of $K _H$, higher with the value of intercept, i.e. partial pressure and it is also for $z$.






