Solid State - Result Question 6
####6. The radius of the largest sphere which fits properly at the centre of the edge of a body centred cubic unit cell is (Edge length is represented by ’ $a$ ‘) (2019 Main, 11 Jan II)
(a) $0.134 a$
(b) $0.027 a$
(c) $0.047 a$
(d) $0.067 a$
Show Answer
Answer:
Correct Answer: 6. (d)
Solution:
- For body centred cubic bcc structure,
radius $(R)=\frac{\sqrt{3}}{4} a$
Where, $a=$ edge length
According to question, the structure of cubic unit cell can be shown as follows:
$\therefore \quad a=2(R+r)$
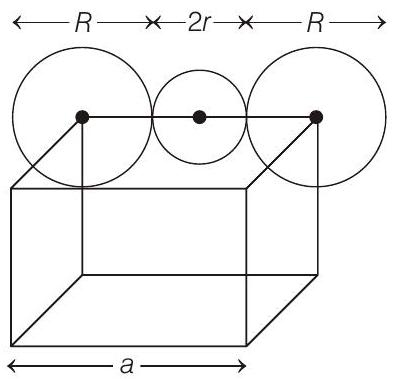
On substituting the value of $R$ from Eq. (i) to Eq. (ii), we get
$$ \frac{a}{2}=\frac{\sqrt{3}}{4} a+r $$
$$ \begin{aligned} & r=\frac{a}{2}-\frac{\sqrt{3}}{4} a=\frac{2 a-\sqrt{3} a}{4} \ & r=\frac{a(2-\sqrt{3})}{4} \ & r=0.067 a \end{aligned} $$
