Solid State - Result Question 3
####3. Consider the bcc unit cells of the solids 1 and 2 with the position of atoms as shown below. The radius of atom $B$ is twice that of atom $A$. The unit cell edge length is $50 %$ more is solid 2 than in 1 . What is the approximate packing efficiency in solid 2?
(2019 Main, 8 April II)
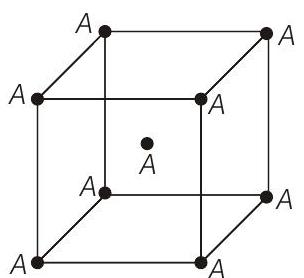
Solid 1
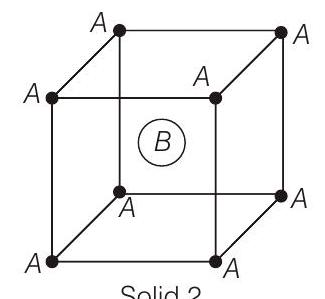
Solid 2
(a) $65 %$
(b) $90 %$
(c) $75 %$
(d) $45 %$
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
Key Idea Packing efficiency
$$ =\frac{\text { Volume occupied by sphere }}{\text { Volume of cube }} \times 100 $$
Given,
$$ \begin{gathered} r _B=2 r _A \ a _2=a _1+\frac{50}{100} a _1=1.5 a _1 \end{gathered} $$
For bcc lattice
$$ \begin{aligned} 4 r _A & =\sqrt{3} a _1 \ r _A & =\frac{\sqrt{3} a _1}{4} \ a _1 & =\frac{4 r _A}{\sqrt{3}} \ \therefore \quad a _2 & =1.5\left(\frac{4 r _A}{\sqrt{3}}\right) \ & =\frac{3}{2}\left(\frac{4 r _A}{\sqrt{3}}\right) \end{aligned} $$
$a _2=2 \sqrt{3} r _A$ Packing efficiency $=\frac{\frac{4}{3} \pi r _A^{3} \times z _A+\frac{4}{3} \pi r _B^{3} \times z _B}{a _2^{3}}$
[As the atoms $A$ are present at the edges only $z _A=\frac{1}{8} \times 8=1$, atom $B$ is present only at the body centre $z _B=1$ ]
$$ \begin{aligned} \therefore \quad PE _2 & =\frac{\left(\frac{4}{3} \pi r _A^{3} \times 1\right)+\left(\frac{4}{3} \pi r _B^{3} \times 1\right)}{a _2^{3}} \ & =\frac{\frac{4}{3} \pi r _A^{3}+\frac{4}{3} \pi\left(2 r _A\right)^{3}}{\left(2 \sqrt{3} r _A\right)^{3}}=\frac{\frac{4}{3} \pi r _A^{3} \times 9}{8 \times 3 \sqrt{3} r _A^{3}}=\frac{\pi}{2 \sqrt{3}} \ & =90.72 % \approx 90 % \end{aligned} $$
