Coordination Compounds 2 Question 7
####8. The calculated spin only magnetic moments (BM) of the anionic and cationic species of $\left[Fe\left(H _2 O\right) _6\right] _2$ and $\left[Fe(CN) _6\right]$, respectively, are
(a) 0 and 4.9
(b) 2.84 and 5.92
(c) 0 and 5.92
(d) 4.9 and 0
(2019 Main, 8 April II)
Show Answer
Solution:
- $\left[Fe\left(H _2 O\right) _6\right] _2 \Rightarrow$ It will form 2 cationic species. i.e.
I. (i) $As\left[Fe\left(H _2 O\right) _6\right]^{2+} \Rightarrow$ High spin octahedral complex of $Fe^{2+}$.
$Fe^{2+}: 3 d^{6}, x=4$ (unpaired electrons)
$$ \mu=\sqrt{4(4+2)} BM=4.9 BM $$
or (ii) as $\left[Fe\left(H _2 O\right) _6\right]^{3+}=$ High spin octahedral complex of $Fe^{3+}$. $Fe^{3+}: 3 d^{5}, x=5, \mu=\sqrt{5(5+2)}=5.92 BM$
[ $H _2 O$ is a neutral weak field ligand] $So,\left[Fe\left(H _2 O\right) _6\right]^{2+}$ will be the cationic specie, $\mu=4.9 BM$. $\left[Fe(CN) _6\right]$ will have two anionic complexes
II. (i) $\left[Fe(CN) _6\right]^{4-} \Rightarrow$ Low spin, octahedral complex of $Fe^{2+}$.
As $CN^{-}$is a strong ligand it will pair up the electrons.
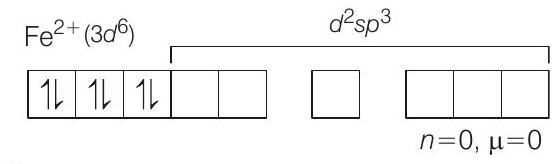
or, (ii) $\left[Fe(CNI) _6\right]^{3-} \Rightarrow$ Low spin octahedral complex of $Fe^{3+}$.
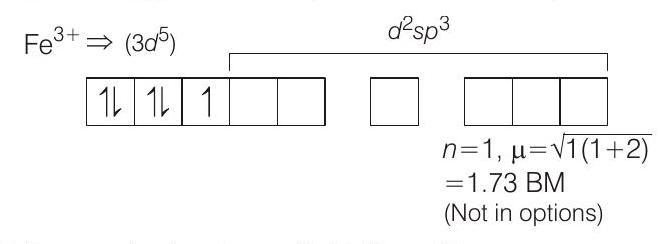
$\left[CN^{-}\right.$is an anionic strong field ligand $]$
So, the anionic species is $\left[Fe(CN) _6\right]^{4-}, \mu=0$
Thus, the calculated spin only magnetic moments (BM) of the anionic and cationic species of $\left[Fe\left(H _2 O\right) _6\right] _2$ and $\left[Fe(CN) _6\right]$ respectively are 4.9 and 0.






