Chemical Kinetics - Result Question 6
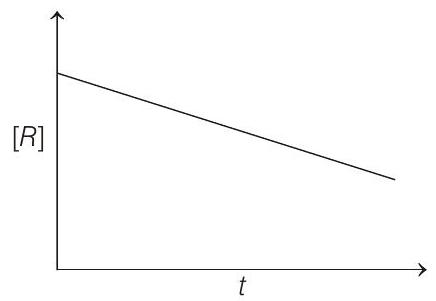
####6. The given plots represent the variation of the concentration of a reaction $R$ with time for two different reactions (i) and (ii). The respective orders of the reactions are
(2019 Main, 9 April I)
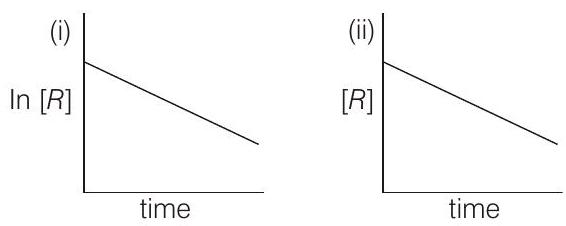
(a) 1,1
(b) 0,2
(c) 0,1
(d) 1,0
Show Answer
Answer:
Correct Answer: 6. (b)
Solution:
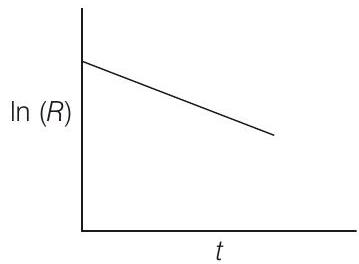
- In first order reaction, the rate expression depends on the concentration of one species only having power equal to unity.
$$ n R \longrightarrow \text { products } $$
$$ \frac{-d[R]}{d t}=k[R] $$
On integration, $-\ln [R]=k t-\ln \left[R _0\right]$
or
$$ \begin{aligned} \ln (R) & =\ln \left(R _0\right)-k t \ y & =c+m x \ m= & \text { slope }=-k(\text { negative }) \ c= & \text { intercept }=\ln \left(r _0\right) \end{aligned} $$
The graph for first order reactions is
In zero order reaction,
$$ \begin{array}{cc} {[R] \longrightarrow \text { product }} \ \therefore \quad & \frac{-d[R] _t}{d t}=k \text { or }-d[R] _t=k d t \end{array} $$
On integrating, $-[R] _t=k t+c$
$$ \begin{array}{ll} \text { If } & t=0,[R] _t=[R] _0 \ \therefore & -[R] _t=k t-[R] _0 \ & {[R] _t=[R] _0-k t} \end{array} $$
Thus, the graph plotted between $[r] _t$ and $t$ gives a straight line with negative slope $(-k)$ and intercept equal to $[R] _0$.
The graph for zero order reaction is