SATHEE: Chemical Kinetics - Result Question 40

Chemical Kinetics - Result Question 40

####40. For a first order reaction $A (g) ⟶ 2 B (g) + C (g)$ at constant volume and $300 K$ , the total pressure at the beginning $(t = 0)$ and at time $t$ are $p_{0}$ and $p_{t}$ , respectively. Initially, only $A$ is present with concentration $[A]_{0}$ , and $t_{1 / 3}$ is the time required for the partial pressure of $A$ to reach $1 / 3^{r d}$ of its initial value. The correct option(s) is (are) (Assume that all these gases behave as ideal gases)

(2018 Adv.) (a)

(c)

(b)

(d)

Show Answer

Answer:

Correct Answer: 40. $(a, d)$

Solution:

Given for the reaction (at $T = 300 K$ and constant volume $= V$ )

$\begin{array}{rrrc} A (g) & ⟶ & 2 B (g) + C (g) at t = 0 & p_{0} & - & - at t = t & p_{0} - x & 2 x & x at t = t_{1 / 3} & [p_{0} - \frac{2 p_{0}}{3}] = \frac{p_{0}}{3} & \frac{4 p_{0}}{3} & \frac{2 p_{0}}{3} \end{array}$

We can calculate,

$\begin{aligned} p_{t} = p_{0} - x + 2 x + x = p_{0} + 2 x & or 2 x = p_{t} - p_{0} or x = \frac{p_{t} - p_{0}}{2} \end{aligned}$

Now for first order reaction,

$t = \frac{1}{k} \ln \frac{p_{0}}{(p_{0} - x)}$

Putting the value of $x$ in the equation,

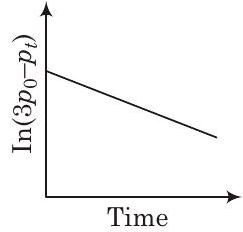
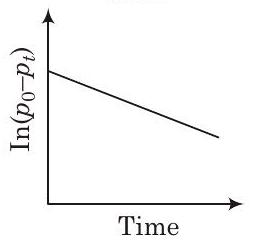
$t = \frac{1}{k} \ln \frac{p_{0}}{p_{0} - (\frac{p_{t} - p_{0}}{2})} = \frac{1}{k} \ln \frac{2 p_{0}}{2 p_{0} - p_{t} + p_{0}}$

$\begin{aligned} or k t = \ln \frac{2 p_{0}}{(3 p_{0} - p_{t})} & or k t = \ln 2 p_{0} - \ln (3 p_{0} - p_{t}) & or \ln (3 p_{0} - p_{t}) = - k t + \ln 2 p_{0} \end{aligned}$

It indicates graph between $\ln (3 p_{0} - p_{t}) v s$ ’ $t$ ’ will be a straight line with negative slope, so option (a) is correct

$t_{1 / 3} = \frac{1}{k} \ln \frac{p_{0}}{p_{0} / 3} = \frac{1}{k} \ln 3$

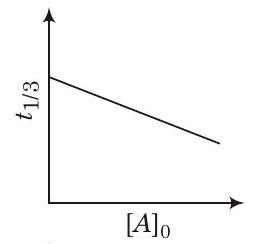
It indicates $t_{1 / 3}$ is independent of initial concentration so, option (b) is incorrect.

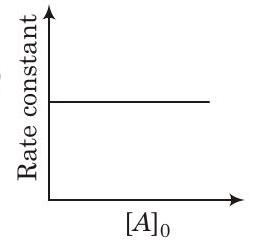
Likewise, rate constant also does not show its dependence over initial concentration. Thus, graph between rate constant and $[A]_{0}$ will be a straight line parallel to $X$ -axis