Chemical Kinetics - Result Question 4
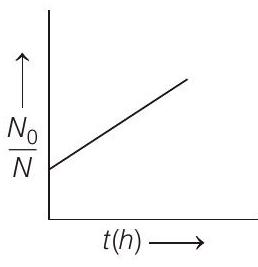
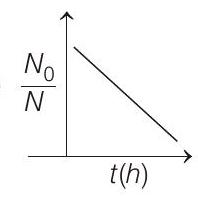
####4. A bacterial infection in an internal wound grows as $N^{\prime}(t)=N _0 \exp (t)$, where the time $t$ is in hours. A dose of antibiotic, taken orally, needs 1 hour to reach the wound. Once it reaches there, the bacterial population goes down as $\frac{d N}{d t}=-5 N^{2}$. What will be the plot of $\frac{N _0}{N} v s t$ after 1 hour?
(2019 Main, 10 April I)
(a)
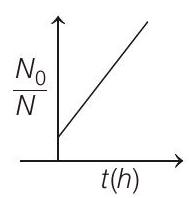
(c)
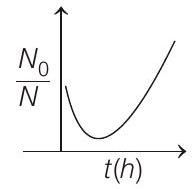
(b)
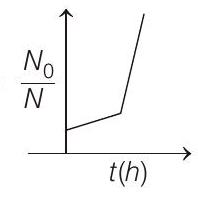
(d)
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- The expression for bacterial growth is
$$ \begin{aligned} N & =N _0 e^{t} \ \frac{N _0}{N} & =e^{-t} \end{aligned} $$
From 0 to 1 hour $N^{\prime}(t)=N _0 e^{t}$
From 1 hour onwards, $\frac{d N}{d t}=-5 N^{2}$
On differentiating the above equation from $N^{\prime}$ to $N$ we get.
$$ \begin{aligned} & \int _{e N _0}^{N} N^{-2} d N=-5 \int _1^{t} d t \quad\left[\because \text { At } 1 \text { hour, } N^{\prime}=e N _0\right] \ & {\left[\frac{1}{N}-\frac{1}{e N _0}\right]=5(t-1)} \end{aligned} $$
Multiply both sides by $N _0$, we get
$$ \begin{aligned} \frac{N _0}{N}-\frac{1}{e} & =5 N _0(t-1) \text { or, } \frac{N _0}{N}=5 N _0(t-1)+\frac{1}{e} \ \frac{N _0}{N} & =5 N _0 t+\left[\frac{1}{e}-5 N _0\right] \end{aligned} $$
On comparing the above equation with equation of straight line, $y=m x+c$
We get $m=5 N _0, c=\frac{1}{e}-5 N _0$
$\therefore$ Plot of $\frac{N _0}{N} v _s t$ is shown aside.