Solution:

Ans. Explanation : As per Huygens’ Principle, net effect at any point $=$ Sum total of contribution of all wavelets with proper phase difference.

1

At the central point $(O)$ the contribution from each half in $S{S}_1$ is in phase with that from the corresponding part in $S_2$. Hence, $\mathrm{O}$ is a maxima.

1

From the figure,

At the point $M$ where $S_{2}M-S_{1}M=\lambda /2$

Phase difference between each wavelet from $S{S}_1$ and corresponding wavelet from $S{S}_2=\lambda /2$

Hence, $M$ would be a minima.

All such points (path difference $=n\lambda /2$ ) are also minima.

Similarly, all points, for which path difference $=(2n+1)\lambda /2$, are maxima but with decreasing intensity.

Half angular width of central maxima $=\lambda /a$

$\therefore$ The size of central maxima will be reduced to half and intensity of central maxima will be four times if slit is made double the original width. $\mathbf{1}$

[CBSE Marking Scheme 2012]

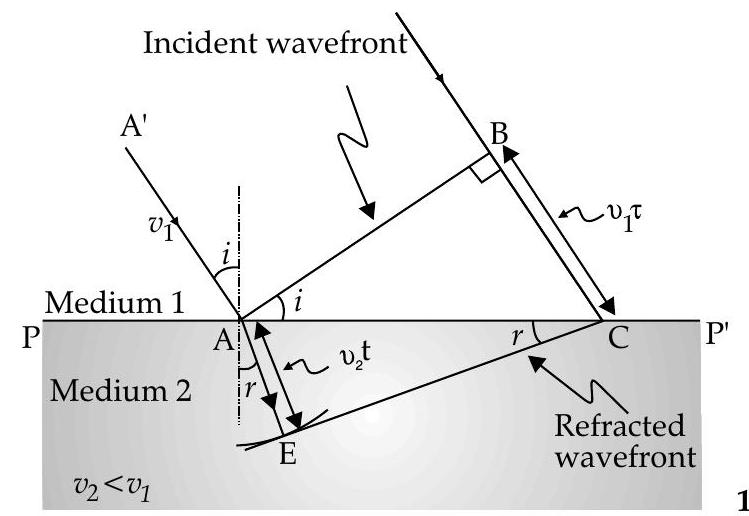
AI Q. 3. (i) State Huygens’ principle. Using it, construct a ray diagram for a plane wavefront getting incident on a denser medium.

(ii) Use Huygens’ principle to prove the laws of reflection of light.

Ans. (i) Huygens principle :

In a wavefront every particle acts as a new source of disturbance which are known as wavelet that travel in every directions with velocity of wave.

The forward (tangential) envelope of all these wavelets at any time gives new wavefront.

(ii)

$AB=$ incident wavefront

$EC=$ reflected wavefront

$\mathrm{\angle }i=$ angle between incident wavefront $AB$ and the interface $AC$.

$\mathrm{\angle }r=$ angle between reflected wavefront $EC$ and the interface $AC$.

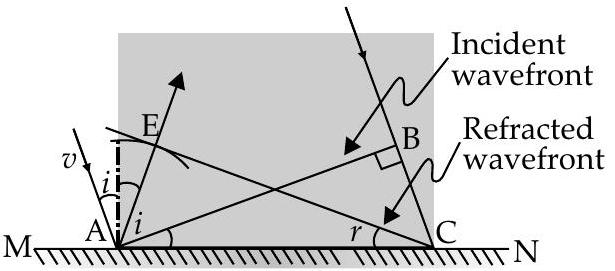
If disturbance at $A$ is reflected from the interface $AC$ then disturbance at $\mathrm{B}$ and disturbance at $A$ both travel in same medium and they will have travelled equal distances in same medium in time $\tau$. Where $\tau$ is the time in which disturbance from $B$ reaches at C.

Now $AE=BC$ (distance travelled in same medium in same time)

$$\mathrm{△}AEC\cong \mathrm{△}ABC$$

$$\mathrm{\angle }i=\mathrm{\angle }r$$

This is law of reflection.

TOPIC-2

Superposition of light waves (hinferference and

Diffraction)

Revision Notes

According to superposition principle, “At a partieular point in the medium, the resultant displacement produced by a number of waves is the vector sum of the displacements produced by each of the waves”.

It means if individual displacement produced at a point by two coherent waves at any instant is given by

Then resultant displacement at that point will be

$$y_1=a\cos \omega t\text{ and }{y}_2=a\cos \omega t\text{. }$$

Hence the total intensity at that point will be :

$y=y_1+y_2=2a\cos \omega t$.

where, $I_0\propto a^2$; maximum intensity due to one wave.

$$I=4I_0$$

Interference

Constructive Interference : If two waves are propagating such that crest and trough of both waves would reaching at a point in the same instant then we say there is constructive interference of two waves at that point and the resultant amplitude of the wave is the sum of individual amplitudes. (We can generalize this to superposition of more than two waves) $a=a_1+a_2$

Destructive Interference : If two waves are propagating such that crest of one wave and trough of other wave reaching at a point in same instant then we say there is destructive interference of two waves at that point. The resultant amplitude of the wave is the difference of individual amplitudes. (We can generalize this to superposition of more than two waves) $a=a_1\sim a_2$

• Two independent sources can never be coherent. We may create two coherent sources by deriving them from one source. Condition for constructive Interference
• Waves would be coherent in nature. Coherent wave means they should have equal frequency and constant phase difference $(0,2\pi ,–2n\pi )$ with each other at any time interval $t$.

Path difference between waves at this phase difference $=0,\lambda ,—-n\lambda$, Here, $n=0,1,2,3$

$$\begin{array}{llllll}\text{ if }& a_r=a_1+a_2\text{ then }& a_1=a_2=a\because & a_r=2a& I\propto a^2& I_r=4a^2\end{array}$$

Condition for destructive interference

Waves would be coherent in nature. The phase diff. of the waves should be odd multiples of $\pi$, i.e., $0,\pi ,\dots .(2n-1)\pi$

Path difference between waves at this phase difference $=\frac{\lambda }{2},\frac{3\lambda }{2},(2n-1)\frac{\lambda }{2}$, Here, $n=1,2,3,4\dots$

$$\begin{array}{llllll}\text{ if }& a_r=a_1-a_2\text{ then }& a_1=a_2\because & a_r=0& I\propto a^2& I_r=0\end{array}$$

Constructive Interference

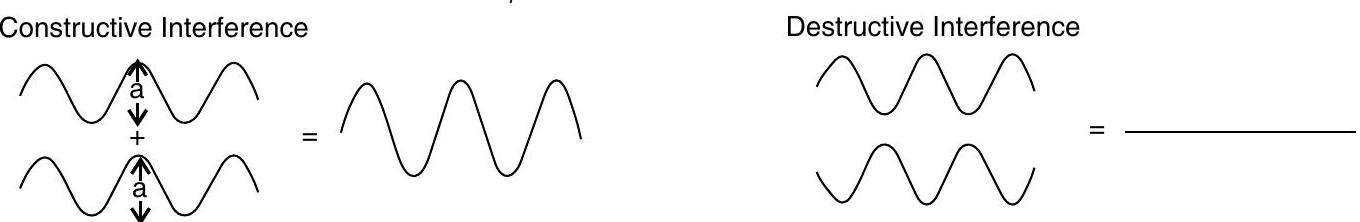
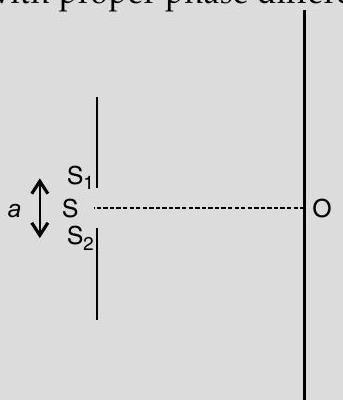
Young’s Experiment

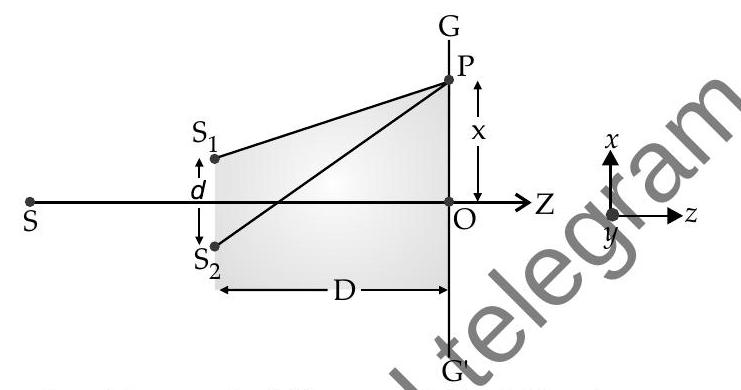
At " $O$ " we would get central maxima. Here path difference $(S_{2}P-S_{1}P)=0$

At " $P$ “, which is at " $x$ " height from " $O$ " path difference $(S_{2}P-S_{1}P)=\frac{xd}{D}$

> Condition for $P$ is a bright spot

$$\begin{array}{rlr}\frac{xd}{D}& =0,\lambda ,2\lambda \dots \dots .n\lambda x_{nth}\text{ bright }& =\frac{nD}{d}\lambda \end{array}$$

where, $n$ is number of bright fringes after central fringe.

• Condition for $\mathbf{P}$ is a dark spot

$$\begin{array}{rlr}\frac{xd}{D}& =0,\frac{3\lambda }{2}—(2n+1)\frac{\lambda }{2}{x}_{n\text{th dark }}& =\frac{(2n+1)D}{2d}\lambda \end{array}$$

Here, $n$ is the number of dark fringes after central fringe.

$>$ Width of the bright fringe $\left({\omega }_B\right)=x_{nB}-x_{(n-1{)}_B}=\frac{D\lambda }{d}$

$>$ Width of the dark fringe $\left({\omega }_D\right)=x_{nD}-x_{(n-1{)}_D}=\frac{D\lambda }{d}$

Didth of the central fringe $\left({\omega }_C\right)=\frac{D\lambda }{d}$

$>$ Hence ${\omega }_B={\omega }_D={\omega }_C$

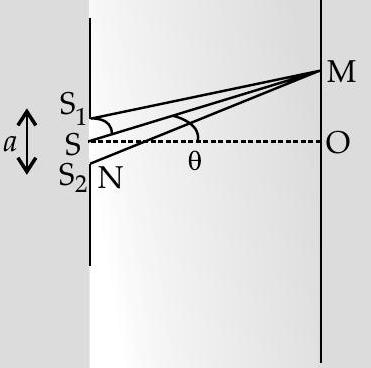
Diffraction

It is defined as the bending of light around the corners of an obstacle or aperture into the region where we should expect shadow of the obstacle.

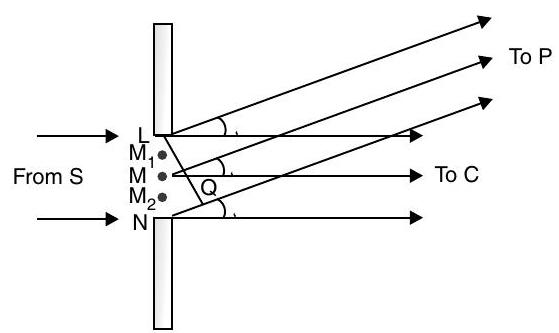
If width of the opening $=a$

$\theta$ is the angle of elevation of point $P$ from principal axis.

Path difference between ray from $L$ and ray from $N=LQ=a\sin \theta$

$$a\sin \theta =\lambda$$

$\because$ for first maxima $\theta =\frac{\lambda }{a}$

It is observed that when path difference $=\lambda ,2\lambda \dots ..(2n-1)\lambda$ then $P$ is a dark point.

When $=a\sin \theta =\frac{3\lambda }{2},\dots ...(2n+1)\frac{\lambda }{2}$ then $P$ is a bright point.

Elevation angle for first bright fringe ${\theta }_{1D}=\frac{3\lambda }{2a}$

Height of first dark fringe $x_{1D}=\frac{3\lambda D}{2a}$

Dlevation angle for first dark fringe ${\theta }_{1D}=\frac{\lambda }{a}$

$>$ Width of the bright fringe $=\frac{D\lambda }{a}$

$>$ Width of the dark fringe $=\frac{D\lambda }{a}$

$>$ Width of the central fringe $=\frac{2D\lambda }{a}$

There is no gain or loss of energy in interference or diffraction, which is consistent with the principle of conservation of energy. Energy only redistributes in these phenomena.

Know the Formulae

Condition for constructive interference for coherent waves

• constant phase difference $(0,2\pi ,—2n\pi )$
• Path difference $=0,\lambda \dots \dots .n\lambda$

Condition for destructive interference for coherent waves

• phase difference $(0,\pi$, — $(2n-1)\pi )$ witheach other at any time interval $t$.
• $$ Path difference $=\frac{\lambda }{2}$, —–(2n-1) $\frac{\lambda }{2}$

In Interference Pattern

• Width of the bright fringe $=\frac{D\lambda }{d}$
• Width of the dark fringe $=\frac{D\lambda }{d}$
• Width of the central fringe $=\frac{D\lambda }{d}$
• (All fringe have equal fringe width)

In Diffraction Pattern

• If angle of elevation of any point $P$ on screen $=\frac{\lambda }{a}$
• Condition that $P$ would be dark point when path difference $=\lambda ,2\lambda \dots ..(2n-1)\lambda$
• Condition that $P$ would be bright point when path difference $=\frac{3\lambda }{2},\dots .(2n+1)\frac{\lambda }{2}$
• Width of the bright fringe $=\frac{D\lambda }{a}$

Width of the dark fringe $=\frac{D\lambda }{a}$

Width of the central fringe $=\frac{2D\lambda }{a}$

• Height of first bright fringe $x_{1B}=\frac{3\lambda D}{2a}$

? Objective Type Questions