Question: Q. 5. Figure shows a system of two polarizing sheets in the path of initially unpolarized light. The polarizing direction of first sheet is parallel to $x$-axis and that of second sheet is $60^{\circ}$ clockwise from $x$-axis. Calculate what fraction of intensity of light emerges from the system.
R [SQP 2016]
Show Answer
Solution:
Ans.
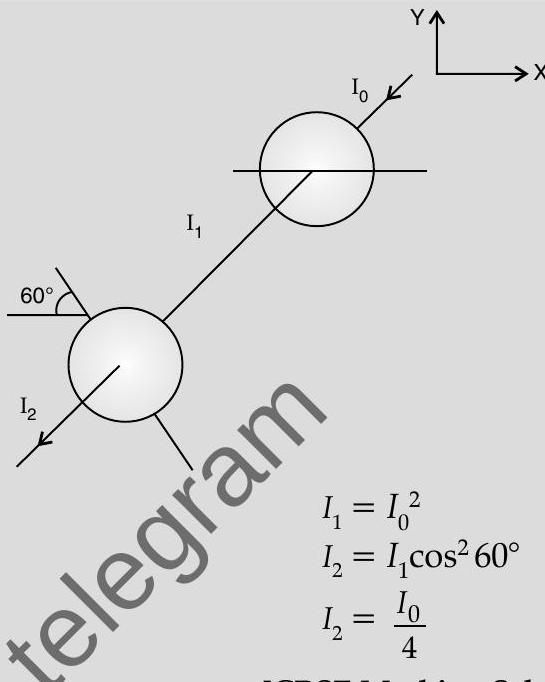
[CBSE Marking Scheme, 2016]
Detailed Answer :
As the axis of first polaroid is parallel to $x$-axis all the light passes through it polarised and passes the second polaroid is at an angle $60^{\circ}$ with the incident light.
$\therefore$ By Malus’ law
$$ \begin{aligned} I_{2} & =I_{1} \cos ^{2} \phi \ & =\frac{1}{2} I_{0} \cos ^{2} 60^{\circ} \ & =\frac{1}{2} \times \frac{I_{0}}{4}=\frac{I_{0}}{8} \end{aligned} $$
[A] Q. 6. Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted intensity be maximum?
R [Delhi I, II, III 2015]
Ans. Let the rotating polaroid sheet makes an angle $\theta$ with the first polaroid.
$\therefore$ Angle with the other polaroid will be $(90-\theta) \quad 1$
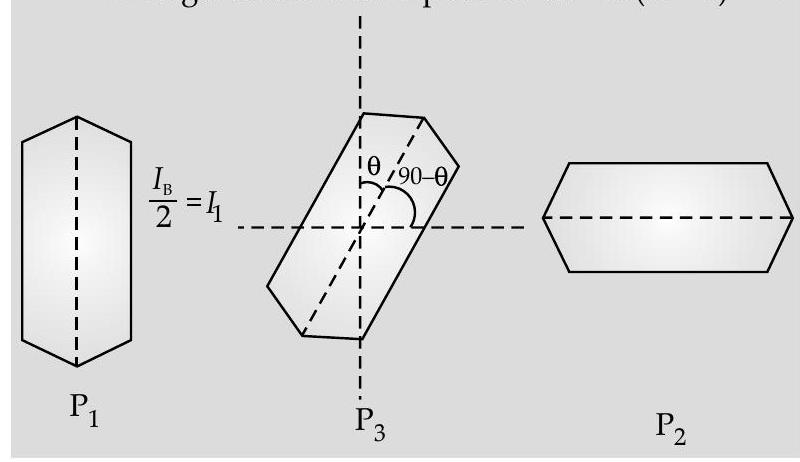
Applying Malus’ law between $P_{1}$ and $P_{3}$
Between $P_{3}$ and $P_{2}$
$$ \begin{aligned} & I_{2}=I_{3} \cos ^{2}\left(\frac{\pi}{2}-\theta\right) \ & I_{2}=\left(I_{1} \cos ^{2} \theta\right) \cos ^{2}\left(\frac{\pi}{2}-\theta\right) \end{aligned} $$
$$ \Rightarrow \quad I_{2}=\frac{I_{1}}{4} \sin ^{2} 2 \theta=\frac{I_{0}}{8} \sin ^{2} 2 \theta \frac{1}{2} $$
$\therefore$ Transmitted intensity will be maximum when
$\theta=\frac{\pi}{4}$
$1 / 2$
[CBSE Marking Scheme 2015]
[Topper’s Answer, 2015]
Short Answer Type Questions-II
(3 marks each)
