Question: Q. 12. When a plane wave front, of light, of wavelength
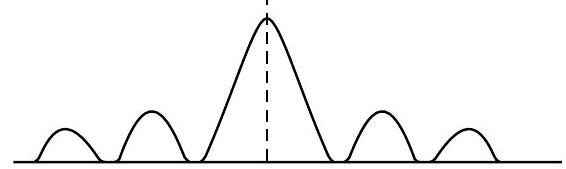
(i) Obtain the conditions for the formation of central maxima and secondary maxima and the minima.
(ii) Why is there significant fall in intensity of the secondary maxima compared to the central maxima, where as in double slit experiment all the bright fringes are of the same intensity?
(iii) When the width of the slit is made double the original width, how is the size of the central band affected?
Show Answer
Solution:
Ans. The phenomenon observed is diffraction.
(i) At the cental maxima : The contributions due to the secondary wavelets, from all parts of the wave front (at the slit), arrive in phase at the central maxima
At the secondary maxima :
It is only the contributions from (Dearly)
1
At the minima :
The contribution, from ‘corresponding pairs’, of the sub-parts of the incident wavefront, cancel each other and the net contribution, at the location of the minima, is zero. The minima occur at points for which,
(ii) There is a significant fall in intensity at the secondary maxima because the intensity there, is only due to the contribution of (nearly)(
(iii) The size of the central maxima would get halved when width of the slit is doubled.
1
[CBSE Marking Scheme 2016]
AT Q. 13. (i) (a) ‘Two independent monochromatic sources of light cannot produce a sustained interference pattern’. Give reason.
(b) Light waves each of amplitude "
(ii) In Young’s double slit experiment, using monochromatic light of wavelength
[Delhi I, II, III 2014 ]
Ans. (i) Try yourself similar to Q. 7 SATQ-II
(ii) A path difference of
A path difference of
[CBSE Marking Scheme 2014]
TOPIC-3
Resolving Power of Optical instruments and Polarisation of Light
Revision Notes
Resolving Power of Optical Instruments : The ability of an optical instrument to separate small or closely adjacent images.
Border line resolving is the required minimum angle 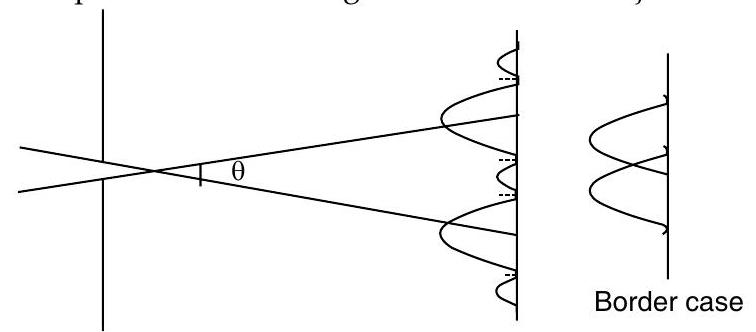
Rayleigh criteria for border line resolving
If opening is circular (which in case of most optical instruments), Rayleigh criteria of border line resolving is
Resolving Power of Microscope
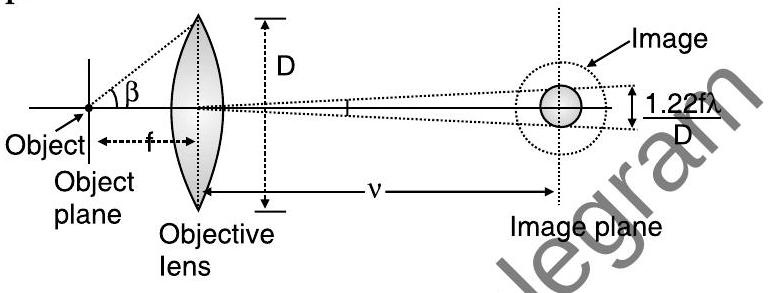
Limit of resolution of microscope
And
Hence to differentiate minimum angular resolution, aperture ’
Fresnel’s distance limit of ray optics
where,
Doppler’s effect
When there is relative motion between source of light and observer, the frequency as apparent to observer is different and there is change, according to the following relation.
where,
If there is redshift in doppler effect then source is moving away and if there is blue shift in doppler effect then source is moving towards observer.
Polarisation
In an unpolarized wave, the displacement will be randomly changing with time though it will always be perpendicular to the direction of propagation.
Hence in unpolarized light wave, vibrations of electric fields are in more than one direction. Polarized light waves are light waves in which the vibrations occur in a single plane.
The process of transforming unpolarized light into polarized light is known as polarisation.
- Light is unpolarized by nature but it may be converted into fully or partial polarized light
The light having oscillation only in one plane is called polarised or plane polarised.
- The plane perpendicular to the plane of oscillation is called plane of polarisation.
Light can be polarised by transmitting through certain crystals such as tourmaline or polaroids.
Polaroids are thin films of ultramicroscopic, crystals of quinine iodo sulphate with their optical axes parallel to each other.
Polaroids allow the light oscillations parallel to the transmission axis to pass through them.
- If an unpolarised light is incident on a polaroid, the transmitted light is plane polarised as shown below :
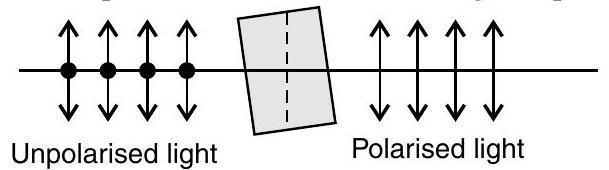
Here, the vertical oscillations are transmitted because the transmission axis is also vertical. The horizontal oscillations are not transmitted. That is why, on the right hand side there are nodots, at the intersection of lines.
- When polaroids are used to convert unpolarised light into polarised they areknown as polarisers.
- When polaroids are used to detect polarised light, they are known as analyse
- If the transmission axes of the polariser and analyser are parallel, then whole of the polarised light passes through the analyser.
If the transmission axis of the analyser is perpendicular to that of polariser, then no light passes through the analyser. Such polariser and analyser are said to be crossed.
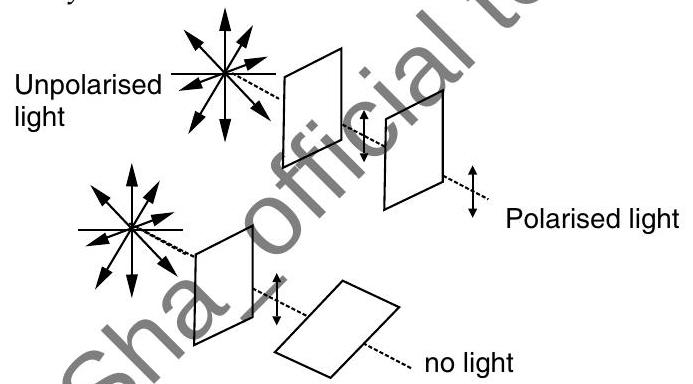
- Malus’ law : It states about thesintensity of a polarised light when it is altered to pass through a polariser at an angle
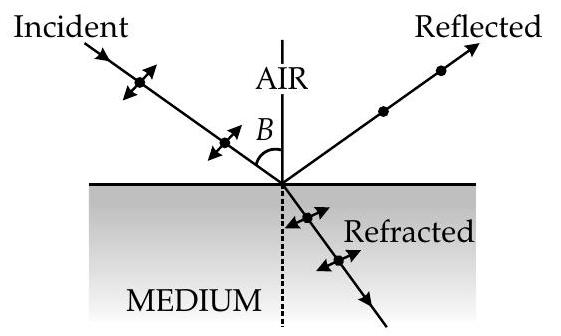
- Polarisation by reflection : When unpolarised light is incident on the boundary between two transparent media such that reflected wave is perpendicular to the refracted wave, then the reflected wave is a totally polarised wave. The angle of incidence in this case is called Brewster’s angle and is denoted by
This is known as Brewster’s law.
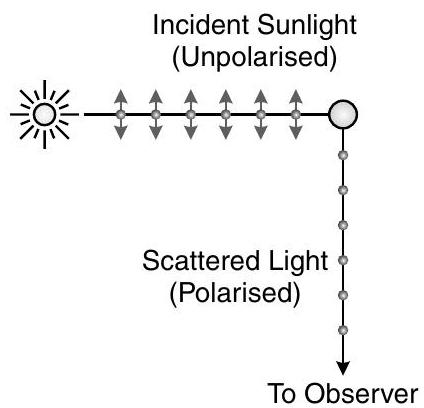
Polarisation by scattering : When scattered light coming to the observer such that source is at
, then scattered light coming to observer is polarised.
Applications of Polarisation :
Polaroids are used to reduce the intensity in window pane, sunglasses etc.
Polaroids are also used in photographic cameras and 3D movie cameras.
Used in making holograms.
Polarisation proves that light is transverse wave.
Chemical analysis of molecules.
Know the Formulae
Resolving Power of Microscope
Resolving Power of Telescope
Polarisation
- Percentage to polarisation is given by






