Question: Q. 9. Answer the following questions :
(i) In a double slit experiment using light of wavelength $600 \mathrm{~nm}$, the angular width of the fringe formed on a distant screen is $0.1^{\circ}$. Find the spacing between the two slits.
(ii) Light of wavelength $5000 \AA$ propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected?
A [Delhi I, II, III 2015]
Show Answer
Solution:
Ans. Finding the spacing between two slits 1 Effect on wavelength and frequency of reflected and refracted width light.
(i) Angular width of fringes :
$$ \theta=\frac{\lambda}{d} $$
where, $d=$ separation between two slits
Here $\theta=0 \cdot 1^{\circ}=0 \cdot 1 \times \frac{\pi}{180}$ radian
$$ \begin{aligned} \therefore \quad d & =\frac{600 \times 10^{-9} \times 180}{0.1 \times \pi} \mathrm{m} \ & =3.43 \times 10^{-4} \mathrm{~m} \ & =0.34 \mathrm{~mm} \end{aligned} $$
(ii) For Reflected light :
Wavelength remains same
Frequency remains same
For Refracted light :
Wavelength decreases
Frequency remains same
[CBSE Marking Scheme 2015]
Detailed Answer :
(b) Incident ray Reflected ray
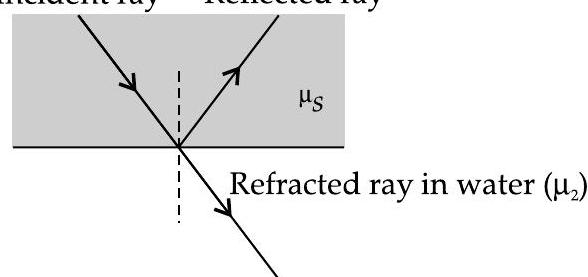
we know that frequency of light is same in all media Thus,
$$ \begin{aligned} f & =\frac{v}{\lambda}=\frac{3.0 \times 10^{8}}{5000 \times 10^{-10}} \ & =0.6 \times 10^{+15} \ & =0.6 \times 10^{15} \mathrm{~Hz} \end{aligned} $$
If wavelength in air is $\lambda_{1} &$ that in water is $\lambda_{2}$.
$$ \begin{aligned} & \mu_{2}=\frac{v_{2}}{v_{1}}=\frac{\lambda_{2}}{\lambda_{1}} \ & \lambda_{2}=\lambda_{1}\left(\frac{\mu_{1}}{\mu_{2}}\right) \ & \lambda_{2}=5000\left(\frac{\mu_{1}}{\mu_{2}}\right) \AA \end{aligned} $$
Wavelength of refracted ray decreases by a factor of $\left(\frac{\mu_{1}}{\mu_{2}}\right)$ while wavelength of reflected ray may remains same.
