Question: Q. 3. Write two points to distinguish between interference and diffraction fringes.
(ii) In a Young’s double slit experiment, fringes are obtained on a screen placed at a certain distance away from the slits. If the screen is moved by $5 \mathrm{~cm}$ towards the slits, the fringe width changes by 30 $\mu \mathrm{m}$. Given that the slits are $1 \mathrm{~mm}$ apart, calculate the wavelength of the light used.
U] [Comptt. 2018]
Show Answer
Solution:
Ans. (a) Two points of difference
$1 / 2+1 / 2$
(b) Formula
Calculation of wavelength
(a) Any two points of difference
| Interference | Diffraction |
|---|---|
| Fringes are equally spaced. |
Fringes are not equally spaced. |
| Intensity is same for all maxima. |
Intensity falls as we go to successive maxima awayfrom the centre. |
| Superposition of two waves originating from two narrow slits. |
Superposition of a con- tinuous family of waves originating from each point on a single slit. |
| Maxima along an an- gle $\lambda / a$ for two narrow slits separated by a distance $a$. |
Minima at an angle of $\lambda / a$ for a single slit of width $a$. |
(b) Let $\mathrm{D}$ be the distance of the screen from the plane of the slits.
We have
Fringe width, $\quad \beta=\frac{\lambda D}{d}$
$1 / 2$
In the first case
$$ \beta=\frac{\lambda D}{d} \text { or } \beta \mathrm{d}=\lambda \mathrm{D} \ldots \text {..(i) } 1 / 2 $$
In the second case
$$ \left(\beta-30 \times 10^{-6}\right)=\frac{\lambda(D-0.05)}{d} $$
$$ \begin{aligned} & \text { or } \quad\left(\beta-30 \times 10^{-6}\right) d=\lambda(D-0.05) \ & 30 \times 10^{-6} \times d=\lambda \times 0.05 \ & \therefore \quad \lambda=\frac{30 \times 10^{-6} \times 10^{-3}}{5 \times 10^{-2}} \mathrm{~m} \ & \therefore \quad \lambda=6 \times 10^{-7} \mathrm{~m}=600 \mathrm{~nm}^{1 / 2} \end{aligned} $$
[AI Q. 4. A monochromatic light of wavelength $\lambda$ is incident normally on a narrow slit of width ’ $a$ ’ to produce a diffraction pattern on the screen placed at a distance $D$ from the slit. With the help of a relevant diagram, deduce the conditions for maxima and minima on the screen. Use these conditions to show that angular width of central maxima is twice the angular width of secondary maxima.
U] [Foreign II 2017]
Ans.
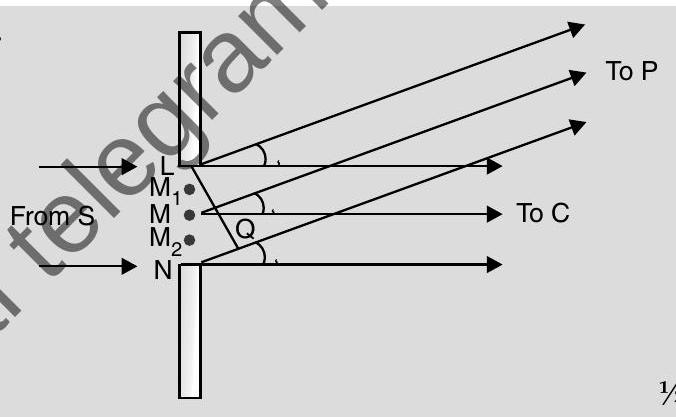
The path difference
$$ \begin{aligned} N P-L P= & N Q \ = & a \sin \theta \cong a \theta \ & \text { as } \theta«<1 \therefore \sin \theta \approx \theta \frac{1 / 2}{2} \end{aligned} $$
By dividing the slit into an appropriate number of parts, we find the point $P$ for which
(i) $\theta=\frac{n \lambda}{a}$ are points of minima.
$1 / 2$
(ii) $\theta=\left(n+\frac{1}{2}\right) \frac{\lambda}{a}$ are points of maxima
$1 / 2$
Angular width of central maxima,
$$ \begin{align*} \theta=\theta_{1}-\theta_{-1} & =\frac{\lambda}{a}-\left(-\frac{\lambda}{a}\right) \ \theta_{2} & =\frac{2 \lambda}{a} \end{align*} $$
Angular width of secondary maxima $=\theta_{2}-\theta_{1}$
$$ =\frac{2 \lambda}{a}-\frac{\lambda}{a}=\frac{\lambda}{a} $$
$=\frac{1}{2} \times$ Angular width of central maxima
$1 / 2$
[CBSE Marking Scheme 2017]
