Question: Q. 4. (i) A giant refracting telescope has an objective lens of focal length $15 \mathrm{~m}$. If an eye piece of focal length $1.0 \mathrm{~cm}$ is used, what is the angular magnification of the telescope?
(ii) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is $3.48 \times 10^{6} \mathrm{~m}$ and the radius of lunar orbit is $3.8 \times 10^{8} \mathrm{~m}$.
A [Delhi I, II, III 2015]
Detailed Answer :
(i) $m=\frac{-f_{0}}{f_{e}}$; ignoring -ve sign as it only shown that image is inverted.
$$ \begin{aligned} & f_{o}=1500 \mathrm{~cm} \ & f_{e}=1 \mathrm{~cm} \ & m=\frac{1500}{1}=1500 \end{aligned} $$
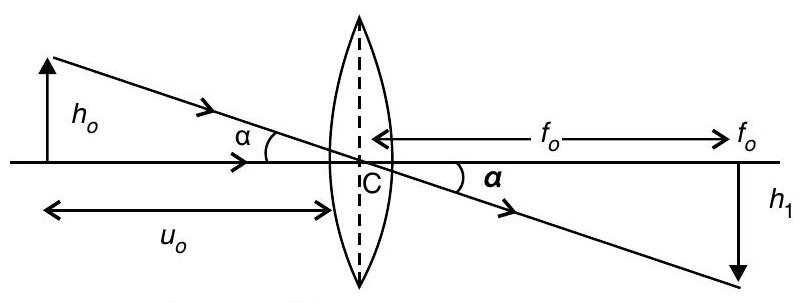
(ii) Angular size of the moon,
$$ \tan \alpha=\frac{h_{0}}{u_{0}} $$
Angular size of the moon’s image by objective lens is also, $\quad \tan \alpha=\frac{h_{1}}{f_{o}}$
Hence,
$$ \begin{aligned} \frac{h_{0}}{u_{0}} & =\frac{h_{1}}{f_{0}} \ h_{o} & =3.48 \times 10^{6} \mathrm{~m} \ u_{o} & =3.8 \times 10^{8} \mathrm{~m} . \ f_{o} & =15 \mathrm{~m} \ \frac{3.48 \times 10^{6}}{3.8 \times 10^{8}} & =\frac{h_{1}}{15} \end{aligned} $$
$$ \begin{aligned} h_{1} & =\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}} \times 15 \ & =13.7 \mathrm{~cm} \end{aligned} $$
Answering Tip
- Learn all the formulae of Telescope carefully. Do practice to solve the humericals by taking care of their sign convention.
Q. 5. (i) Draw a labelled ray diagram showing the formation of a final image by a compound microscope at the least distance of distinct vision.
(ii) The total magnification produced by a compound microscope is 20 . The magnification produced by the eye piece is 5 . The microscope is focussed on a certain object. The distance between the objective and eyepiece is observed to be $14 \mathrm{~cm}$.
If the least distance of distinct vision is $20 \mathrm{~cm}$, calculate the focal length of the objective lens and the eye piece.
A [Delhi I, II, III 2014]
Show Answer
Solution:
Ans. (i) Labelled ray diagram of a compound microscope for formation of image at the near point of the eye :
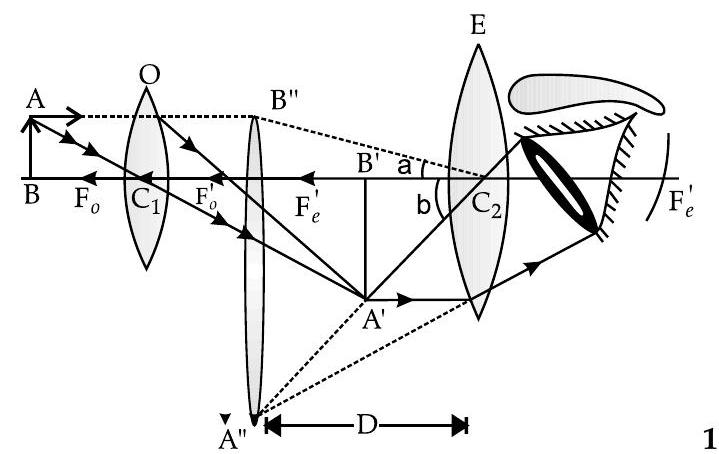
(ii) Given, $m=20, m_{e}=5, \mathrm{D}=20 \mathrm{~cm}$
For eyepiece, $\quad m_{e}=\frac{\mathrm{D}}{u_{e}}$
$$ 5=-\frac{20}{u_{e}} $$
$$ \begin{aligned} u_{e} & =-4 \mathrm{~cm} \ \frac{1}{f_{e}} & =\frac{1}{v_{e}}-\frac{1}{u_{e}} \ & =\frac{1}{-20}+\frac{1}{4} \ \frac{1}{f_{e}} & =\frac{-1+5}{20} \ \frac{1}{f_{e}} & =\frac{4}{20} \ f_{e} & =5 \mathrm{~cm} \end{aligned} $$
Hence, focal length of eyepiece, $f_{e}=5 \mathrm{~cm}$
$$ \begin{aligned} m & =m_{o} \times m_{e} \ m_{o} & =\frac{m}{m_{e}}=\frac{20}{5}=4 \ v_{o} & =14-4=10 \mathrm{~cm} \end{aligned} $$
For objective lens,
$$ \begin{aligned} m_{o} & =-\frac{v_{0}}{u_{o}} \ 4 & =-\frac{10}{u_{o}}\left(\because m_{o}=4\right) \ \Rightarrow \quad u_{o} & =-\frac{10}{4}=-2.5 \mathrm{~cm} \ \text { Now, } \quad \frac{1}{f_{0}} & =\frac{1}{v_{o}}-\frac{1}{u_{0}} \ \frac{1}{f_{0}} & =\frac{1}{10}-\frac{1}{-2.5} \ \frac{1}{f_{0}} & =\frac{1}{10}+\frac{10}{25} \ \frac{1}{f_{0}} & =\frac{1}{2} \ f_{0} & =2 \mathrm{~cm} \end{aligned} $$
Hence, focal length of objective, $f_{0}=2.0 \mathrm{~cm}$.
