Question: Q. 1. (i) Draw a ray diagram to show the image formation by a combination of two thin convex lenses in contact. Obtain the expression for the power of this combination in terms of the focal lengths of the lenses.
(ii) A ray of light passing from air through an equilateral glass prism undergoes minimum deviation when the angle of incidence is
U[OD I, 2017]
Show Answer
Solution:
Ans. (i)
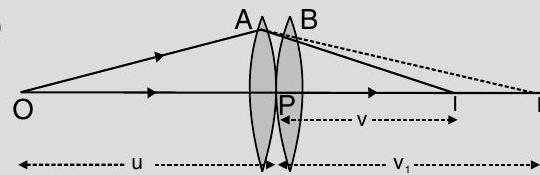
Two thin lenses, of focal length
This image serves as object for the second lens.
Adding, we get
(ii) At minimum deviation
We are given that,
[Award
but does not do any calculations.]
[CBSE Marking Scheme 2017]
AI Q. 2. (i) A point object is placed on the principal axis of a convex spherical surface of radius of curvature
(ii) A converging lens has a focal length of
U] [Foreign 2017]
Ans. (i)
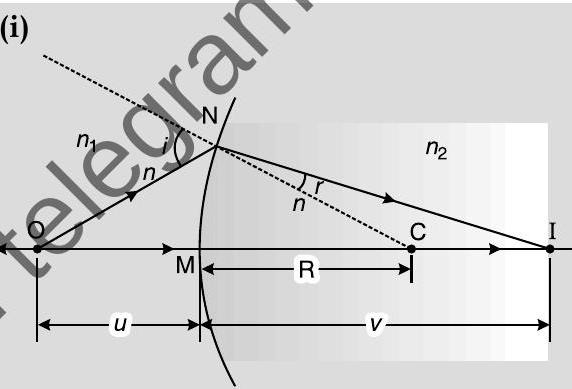
For small angles
For
Similarly,
For small angles, Snell’s law can be written as
(using sign convention)
(ii) Lens maker’s formula is
Focal length of lens is
Let
Or
[CBSE Marking Scheme 2017]






