Question: Q. 4. A symmetric biconvex lens of radius of curvature and made of glass of refractive index 1.5 , is placed on a layer of liquid placed on top of a plane mirror as shown in the figure. An optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle from the lens is measured to be . On removing the liquid layer and repeating the experiment, the distance is found to be . Obtain the expression for the refractive index of the liquid in terms of and .
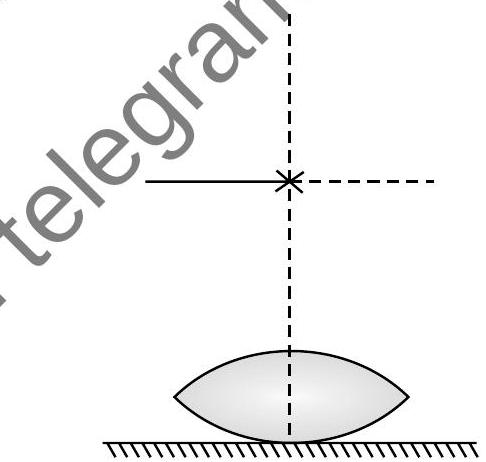
[Delhi & OD 2018; Delhi Comptt. 2014]
Show Answer
Solution:
Ans. Lens maker’s formula Formula for ‘combination of lenses’ Obtaining the expression for
(a) Let denote the refractive index of the liquid. When the image of the needle coincides with the lens itself; its distance from the lens, equals the relevant focal length.
With liquid layer present, the given set up, is equivalent to a combination of the given (convex) lens and a concavo plane/plano concave ’liquid lens’.
We have
and
as per the given data,
[CBSE Marking Scheme 2018]
Detailed Answer :
Given, Radius of curvature of convex lens is and
When lens is placed on a layer of water then focal length of combination is . Thus the first measurement gives the focal length of combination i.e. .
In second measurement, we get the focal length of convex lens i.e., , therefore the focal length of plano convex lens of water is given as
For plano convex lens of liquid of refractive index

Now from eqn. (i) and (ii),
Now again for plano convex lens of air, if image coincide at then for case II we have
Now from eqn. (iii) and (iv),
This is the required expression for the refractive index of liquid.








