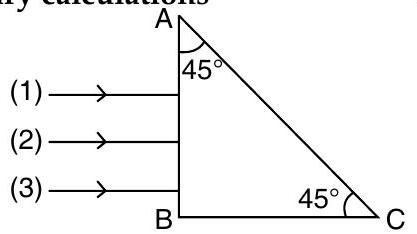
Question: Q. 3. Three rays of different colours fall normally on one of the sides of an isosceles right angled prism as shown. The refractive index of prism for these rays is and 1.52 respectively. Find which of these rays get internally reflected and which get only refracted from AC. Trace the paths of rays. Justify your answer with the help of necessary calculations
U] [OD 2017]
Show Answer
Solution:
Ans. At plane , the incident angle for ray 1 , ray 2 and ray
Let critical angle for total internal reflection for ray
Hence
Let critical angle for total internal reflection for ray
Hence
Let critical angle for total internal reflection for ray
Hence
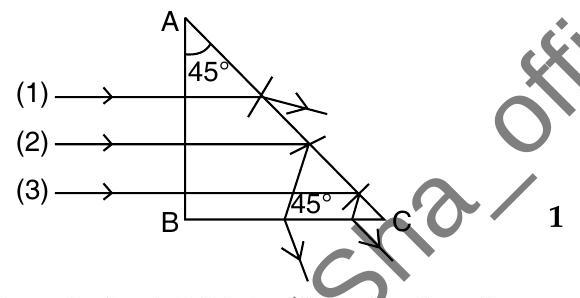
As in case of ray 1 , incident angle is less than critical angle, it would emerge out from . In the figure path of the ray 1 is shown.
In case of ray 2 , ray 3 , incident angle is greater than critical angle, they would get total internal reflection at and emerge from . In the figure path of the ray 2 and 3 are shown.








