Question: Q. 7. A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of $80 \mathrm{~cm}$. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of the refractive index of water to be $\frac{4}{3}$. A [Delhi Comptt. I, II, III 2013]
Show Answer
Solution:
Ans. Actual depth of the bulb in water, $\left(d_{1}\right)=0.8 \mathrm{~m}$
Refractive index of water, $\mu=\frac{4}{3}$
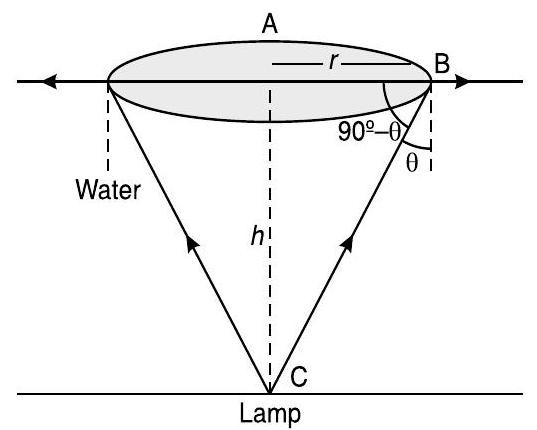
Where, Angle of incidence $=\theta$
Angle of refraction $=90^{\circ}$
Since the bulb is a point source, the emergent light can be considered as a circle of radius $r$
$$ \begin{aligned} \mu & =\frac{\sin 90^{\circ}}{\sin i} \ \frac{4}{3} & =\frac{\sin 90^{\circ}}{\sin \theta} \ \sin \theta & =\frac{3}{4} \ \cos \theta & =\sqrt{1-\sin ^{2} \theta}=\frac{\sqrt{7}}{4} \ \tan \theta & =\frac{3}{\sqrt{7}} \end{aligned} $$
From the figure $\tan \theta=\frac{r}{h}$
$$ \frac{3}{\sqrt{7}}=\frac{r}{0.8} $$
$\therefore$
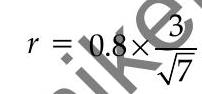
Area of the surface of water through light emerge $=\pi r^{2}=\pi(0.91)^{2}=2.6 \mathrm{~m}^{2}$
Hence, the area of the surface of water through which the light from the bulb can emerge is approximately $2.6 \mathrm{~m}^{2}$.
1
[A] Q. 8. Two monochromatic rays of light are incident normally on the face $A B$ of an isosceles rightangled prism $A B C$. The refractive indices of the glass prism for the two rays ’ 1 ’ and ’ 2 ’ are respectively 1.35 and 1.45 . Trace the path of these rays after entering through the prism.
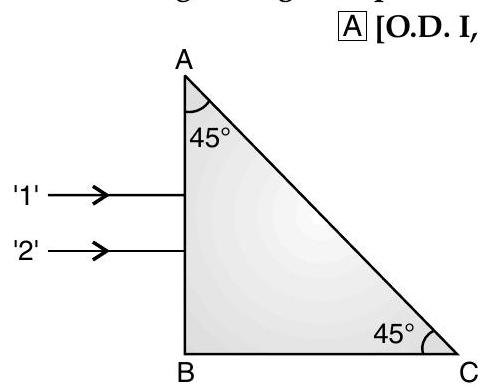
Ans.
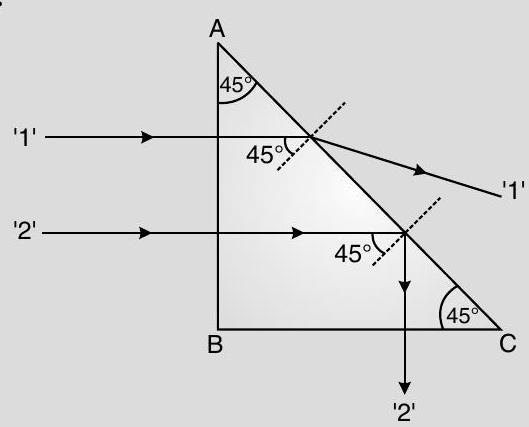
[CBSE Marking Scheme 2014]
