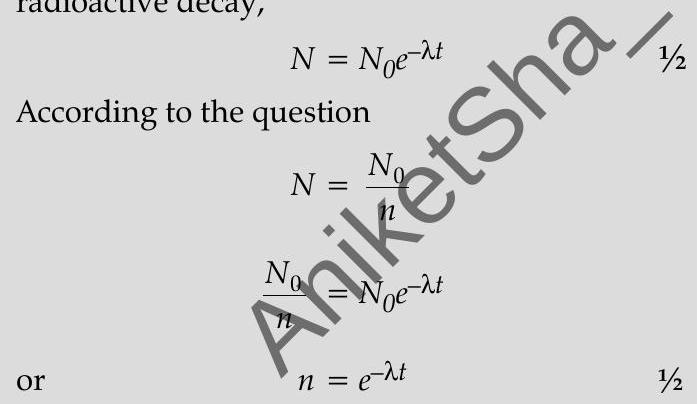Question: Q. 12. (i) The number of nuclei of a given radioactive nucleus, at times $t=0$ and $t=T$, are $N_{0}$ and $\left(N_{0} / n\right)$ respectively. Obtain an expression for the half life $\left(T_{1 / 2}\right)$ of this nucleus in terms of $n$ and $T$.
(ii) Identify the nature of the ‘radioactive radiations’, emitted in each step of the ‘decay chain’ given below :
$$ { }^{A} X_{Z} \rightarrow{ }^{A-4} Y_{Z-2} \rightarrow{ }^{A-4} Y_{Z-2} \rightarrow{ }^{A-4} W_{Z-1} $$
U] [SQP 2013]
Show Answer
Solution:
Ans. (i) According to the (exponential) law of radioactive decay,
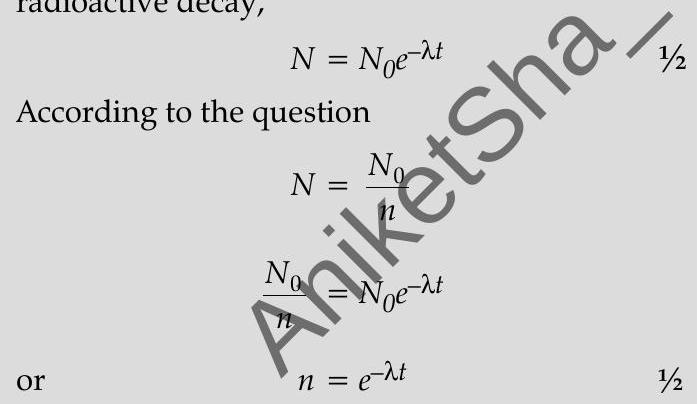
Taking $\log$ on both sides
$$ \begin{array}{rlrl} \ln n & =-\lambda t \ & \text { Now given } & t & =T \ & \text { and } \quad \lambda & =\frac{0.693}{T_{1 / 2}} \ & \frac{\ln n}{T} & =\frac{0.693}{T_{1 / 2}} \ \therefore & T_{1 / 2} & =\frac{0.693 T}{\ln n} \tag{1} \end{array} $$
(ii) In ${ }^{A} X_{Z} \rightarrow{ }^{A-4} Y_{Z-2}$; Mass number changes by 4 units and atomic number changes by 2 units. Hence, it is $\alpha$-decay. In ${ }^{A-4} \mathrm{Y}{\mathrm{Z}-2} \rightarrow{ }^{A-4} Y{\mathrm{Z}-2}$; there is no change in mass number and atomic number. Hence it is $\gamma$ - decay.
In ${ }^{A-4} Y_{Z-2} \rightarrow{ }^{A-4} W_{Z-1}$; there is no change in mass number and +1 change in atomic number. Hence this is $\beta^{-}$decay.
[CBSE Marking Scheme 2013]
