Question: Q. 8. Half life of ${ }_{92}^{238} \mathrm{U}$ against $\alpha$-decay is $4.5 \times 10^{9}$ years.
Calculate the activity of 1 gram sample of ${ }_{92}^{238} \mathrm{U}$ ?
Given Avagadro’s number $=6 \times 10^{26}$ atoms/ kmol. U] [OD East 2016]
Show Answer
Solution:
Ans. Activity,
$$ \begin{align*} R & =\lambda N \ & =\frac{0.693}{\mathrm{~T}_{1 / 2}} N \ R & =\frac{0.693}{1.42 \times 10^{17}} \times N \tag{1} \end{align*} $$
Activity,
Number of nuclei present in 1 gram sample of ${ }_{92}^{238} \mathrm{U}=2503 \times 10^{20}$
$$ \begin{aligned} \Rightarrow \quad R & =\frac{0.693}{1.42 \times 10^{17}} \times \frac{6.0 \times 10^{26}}{238 \times 10^{3}} s^{-1} \ & =1.23 \times 10^{4} \mathrm{~s}^{-1} \end{aligned} $$
[CBSE Marking Scheme 2016]
Detailed Answer :
$238 \mathrm{~g}$ of Uranium $=1$ mole atoms
According to the question
$238 \times 10^{3} \mathrm{~g}$ of sample Uranium contain
$$ =6 \times 10^{26} \text { atoms } $$
$1 \mathrm{~g}$ of sample Uranium contain
$$ \begin{aligned} & =\frac{6 \times 10^{26}}{238 \times 10^{3}} \ & =2.52 \times 10^{21} \text { atoms } \end{aligned} $$
Activity, $\quad R=\lambda N$
where,
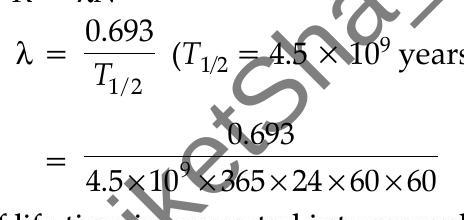
(half life time is converted into seconds)
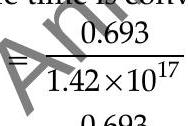
Hence,
$$ \begin{align*} & R=\frac{0.693}{1.42 \times 10^{17}} \times 2.52 \times 10^{21} \ & R=1.23 \times 10^{4} \mathrm{~s}^{-1} \tag{1} \end{align*} $$
