Question: Q. 8. Draw a plot of potential energy of a pair of nucleons as a function of their separations. Mark the regions where the nuclear force is (i) attractive and (ii) repulsive. Write any two characteristic features of nuclear forces.
Show Answer
Solution:
Ans.
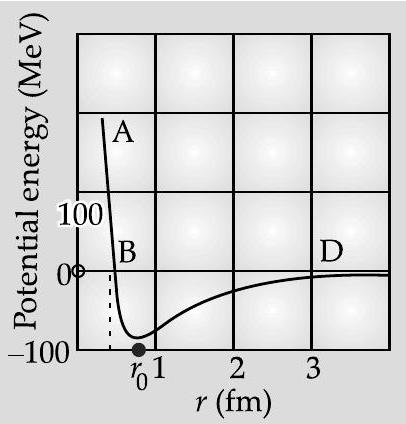
For
For
(i) Nuclear forces are very strong. They are much stronger as compared to gravitational or coulomb forces.
(ii) They are chafgeindependent forces.
1
[CBSE Marking Scheme 2012]
TOPIC-2
Radioactivity and Nuclear Reactor
Revision Notes
- Radioactivity: When atoms become very heavy, neutrons are unable to bind and some nucleons keep on leaving the nucleus. These atoms/elements are known as radioactive elements and process of spontaneous ejection of nucleons or radiations is known as radioactivity.
There are three types of radiodactive decay in nature.
- After
Examples :
$$ \begin{gathered} { }{Z}^{A} \mathrm{X} \rightarrow{ }{\mathrm{Z}-2}^{A-4} \mathrm{Y}+{ }{2}^{4} \mathrm{He} \ { }{92}^{238} \mathrm{U} \rightarrow{ }{90}^{234} \mathrm{Th}+{ }{2}^{4} \mathrm{He} \end{gathered} $$
- The difference between the initial mass energy product and the final mass energy of the decay products is called the
Properties of
- The velocity of
- In
Properties of
- In beta minus
Example :
$$ { }{15}^{32} \mathrm{P} \rightarrow{ }{16}^{32} \mathrm{~S}+{ }{-1} e^{0}+\bar{v} \quad\left(T{1 / 2}=14.3 d\right) $$
- In beta plus
Example :
$$ { }{11}^{22} \mathrm{Na} \rightarrow{ }{10}^{22} \mathrm{Ne}+{ }{1} e^{0}+v \quad\left(T{1 / 2}=2.6 y\right) $$
- In these equations
- The velocity of
Properties of
- There are energy levels in nucleus also.
- When a excited state nucleus makes a transition to a lower energytate, it radiate electromagnetic radiation. As the energy differences between levels in a nucleus are of theorder of
- Most radionuclides after an alpha decay or a beta decay leave the daughter nucleus in an excited state. Then this excited daughter nucleus come to ground state by fatiating
Laws of Radioactive decay :
- Rate of decay
where,
For very small time interval
where,
Integrating on bothsides,
- Rate of disintegration, Differentiating
Often rate of disintegration
Alternative form of law of Radioactive decay:
where,
The SI unit for rate of radioactive decay is becquerel. One becquerel
Measurement of life of radionuclide :
- Half lifetime
D Mean life
Relation between half life time and mean life :
We may also derive from above formulae of half lifetime and radioactive decay rate that
where,
Nuclear Energy by artificial Fission and Fusion processes
- Fission : When a heavy nucleus is broken into two smaller nuclei, the process is known as fission. In this process huge amount of energy is released.
When a neutron was bombarded on a uranium target, the uranium nucleus broke into two nearly equal fragments releasing huge amount of energy.
- Some combination of products of above reaction are
$$ \begin{aligned} & { }{0}^{1} n+{ }{92}^{235} \mathrm{U} \rightarrow{ }{92}^{236} \mathrm{U} \rightarrow{ }{56}^{144} \mathrm{Ba}+{ }{36}^{89} \mathrm{Kr}+3{ }{0}^{1} n \ & { }{0}^{1} n+{ }{92}^{235} \mathrm{U} \rightarrow{ }{92}^{236} \mathrm{U} \rightarrow{ }{51}^{133} \mathrm{Ba}+{ }{41}^{99} \mathrm{Nb}+4{ }{0}^{1} n \ & { }{0}^{1} n+{ }{92}^{235} \mathrm{U} \rightarrow{ }{54}^{140} \mathrm{Xe}+{ }{38}^{94} \mathrm{Sr}+2{ }_{0}^{1} n \end{aligned} $$
- The energy released (the
Nuclear Reactor :
- When ${ }{92}^{235} \mathrm{U}
form of chain reaction is used in nuclear reactor.
- Reason for not having a chain reaction in efficient way
- Poor concentration of Uranium
Solution : Enrichment of ore.
- Speed of neutrons is very high hence theypenetrate through Uranium, without having fission reaction.
Solution : Convert high energy neutron to thermal neutron by collision with moderator.
- Controlling the rate of reaction.
Solution : Insertion of controlrods so that they absorb excess neutrons and rate of reaction
Benefits of Nuclear reactor :
- Huge energy from small quantity of uranium. It’s a good replacement of coal reactor.
Risks of Nuclear reactor :
- Uncontrollable blast
- Radiation leakage Oranium waste is also radioactive.
Nuclear Fusion: Two light nuclei (low Binding Energy per Nucleon) join and form one nucleus of higher Binding Energy per Nucleon, energy is released. This process is known as Fusion.
Some Examples of nuclear fusion are
$$ \begin{aligned} & { }{1}^{1} \mathrm{H}+{ }{1}^{1} \mathrm{H} \rightarrow{ }{1}^{2} \mathrm{H}+e^{+}+v+0.42 \mathrm{MeV} \ & { }{1}^{2} \mathrm{H}+{ }{1}^{2} \mathrm{H} \rightarrow{ }{2}^{3} \mathrm{He}+n+3.27 \mathrm{MeV} \ & { }{1}^{2} \mathrm{H}+{ }{1}^{2} \mathrm{H} \rightarrow{ }{1}^{3} \mathrm{H}+{ }{1}^{1} \mathrm{H}+4.03 \mathrm{MeV} \end{aligned} $$
Stars have fusion energy.
- Fusion process gives more energy than fission process. In the above examples of fusion and fission, energy from one unit mass by fusion is
Advantages of Nuclear fusion reactor :
- It’s a clean fuel. No radioactive wastage in this process.
- Hydrogen is available in plenty.
Problems of Nuclear fusion reactor:
- Cannot be stopped unless the whole stock is burnt.
- Storage of hydrogen plasma.
Hydrogen bomb is uncontrollable nuclear fusion reaction.
Thermal nuclear fusion reaction in Sun : Fusion of hydrogen nuclei into helium nuclei is the source of energy of all stars including our sun.
$$ \begin{equation*} { }{1}^{1} \mathrm{H}+{ }{1}^{1} \mathrm{H} \rightarrow{ }_{1}^{2} \mathrm{H}+e^{+}+v+0.42 \mathrm{MeV} \tag{i} \end{equation*} $$
$$ \begin{align*} e^{+}+e^{-} & \rightarrow \gamma+\gamma+1.02 \mathrm{MeV} \tag{ii}\ { }{1}^{2} \mathrm{H}+{ }{1}^{1} \mathrm{H} & \rightarrow{ }{2}^{3} \mathrm{He}+\gamma+5.49 \mathrm{MeV} \tag{iii}\ { }{2}^{3} \mathrm{H}+{ }{2}^{3} \mathrm{H} & \rightarrow{ }{2}^{4} \mathrm{He}+{ }{1}^{1} \mathrm{H}+{ }{1}^{1} \mathrm{H}+12.86 \mathrm{MeV} \tag{iv} \end{align*} $$
The combined effect of above reactions is
$$ 4{ }{1}^{1} \mathrm{H}+2 e^{-} \rightarrow{ }{2}^{4} \mathrm{He}+2 v+6 \gamma+26.7 \mathrm{MeV} $$
Know the Formulae
Law of Radioactive decay :
Rate of disintegration
or
Alternative form of law of Radioactive decay:
Measurement of life of radionuclide :
Half lifetime
Mean life :
? Objective Type Questions
where,






