Question: Q. 5. Draw a plot of $B E / A$ versus mass number $A$ for $2 \leq A \leq 170$. Use this graph to explain the release of energy in the process of nuclear fusion of two light nuclei. U] [Delhi Comptt. I, II, III 2014]
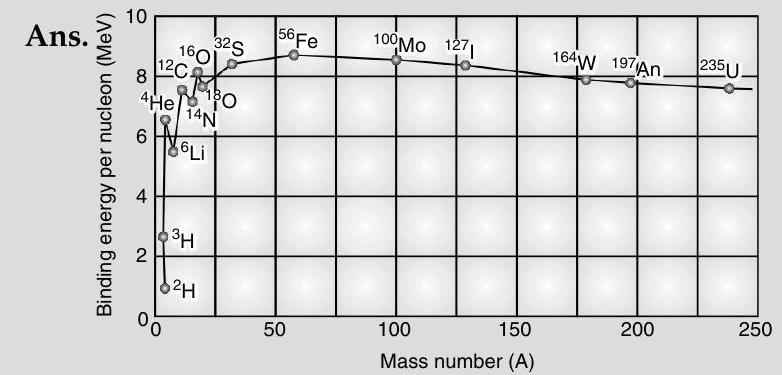
From the above graph, its clear that binding energy per nucleon is low for very light nuclei ( approximate below 20 mass number), if two very light nuclei $(A \leq 10)$ join and form a heavier nucleus. Then from the graph we may deduce that binding energy per nucleon of the fused heavier nuclei is more than the binding energy per nucleon of the lighter nuclei. More binding energy per nucleon means final system is more tightly bound than the initial system and energy would be released in such a process. This is the reason that energy is released in the process of fusion of two light nuclei.
$1+1=2$
[CBSE Marking Scheme 2014]
Answering Tip
- Remember $B E / A$ for few important elements like Fe and overall nature of the curve. Then it wilube easy to draw the graph.
Q. 6. Show that the density of nucleus over a wide range of nuclei is constant and independent of mass number. U[Delhi I, II, III 2013; Delhi I, II, III 2012]
Show Answer
Solution:
Ans. We have
$\therefore$ Density,
$$ \begin{align*} R & =R_{0} A^{1 / 3} \ \rho & =\frac{m A}{\frac{4}{3} \pi\left(R_{0} A^{1 / 3}\right)^{3}} \ & =\frac{m}{\frac{4}{3} \pi R_{0}^{3}} \end{align*} $$
Hence $\rho$ is independent of $A$.
(Here $m$ is the mass of the nucleus.)
$1 / 2$
[CBSE Marking Scheme 2013]
Detailed Answer :
mass of nucleus $M=$ volume of nucleus $\times$ nucleus
$$ \begin{aligned} M= & V \times \rho \ M= & \frac{4}{3} \pi R^{3} \rho \ & (R=\text { radius of the nucleus }) \ R^{3}= & \frac{3 M}{4 \pi \rho} \end{aligned} $$
$$ \begin{equation*} R=\left(\frac{3}{4 \pi \rho}\right)^{\frac{1}{3}} M^{\frac{1}{3}} \tag{i} \end{equation*} $$
If $m=$ mass of one nucleon then mass of nucleus $M=m A$ where $A=$ mass number $(Z+N)$
Putting the value of $M$ in eq. (i)
$$ R=\left(\frac{3}{4 \pi \rho}\right)^{\frac{1}{3}}(m A)^{\frac{1}{3}} $$
We know that
$$ R=R_{0} A^{\frac{1}{3}} $$
Hence,
$$ R_{0} A^{\frac{1}{3}}=\left(\frac{3}{4 \pi \rho}\right)^{\frac{1}{3}}(m A)^{\frac{1}{3}} $$
Cubing both sides
$$ R_{0}^{3} A=\frac{3}{4 \pi \rho} m A $$
Or $\rho=\frac{3 m}{4 \pi R_{0}^{3}}$
Hence proved that Nuclear density $\rho$ over a wide range of nuclei is constant and independent of mass number $A$.
(i) The mass of a nucleus in its ground state is always less than the total mass of its constituents neutrons and protons. Explain.
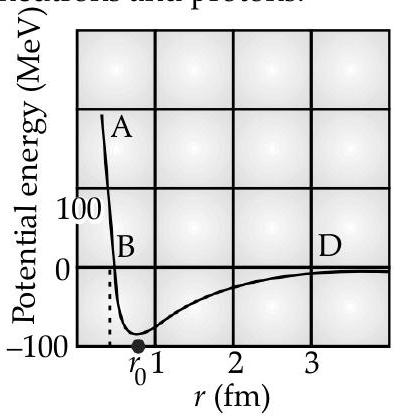
(ii) Plot a graph showing variation of potential energy of a pair of nucleons as a function of their separation.
U] + R [OD 2009]
Ans. (i) Protons and neutrons have to come very near to bind together and form a nucleus. This distance is of the order of $10^{-14} \mathrm{~m}$. In order to achieve this distance a lot of energy is required. The required energy is provided by the nucleon at the expense of some portion of their masses. This is the reason that the mass of a nucleus in its ground state is always less than the total mass of its constituents neutrons and protons.
(ii)
$1+1=2$
Commonly Made Error
- Most of the students couldn’t write the correct reasoning.
- They wrote that mass of a nucleus is always less than the total mass of its constituents and energy is released if it is converted to a nucleus of high $B E / A$.
