Question: Q. 1. (i) State Ampere’s circuital law. Consider a long straight wire of a circular cross-section (radius
(ii) The current
R [SQP I 2017]
Show Answer
Solution:
Ans. (i) Ampere’s circuital law states that the line integral
of magnetic field around a closed path is
total current enclosed by the path,
where,

Magnefic field at a point will not depend on the
shape of Amperian loop and will remain same at every point on the loop.
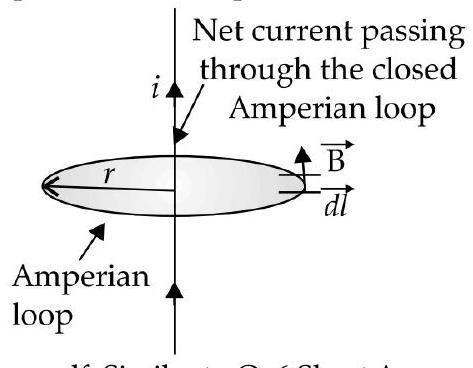
(ii) Try yourself, Similar to Q. 6 Short Answer Type-II
AI] Q. 2. (i) State Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius , having ’
(ii) An observer to the left of a solenoid of
R U [Delhi I, II, III 2015]
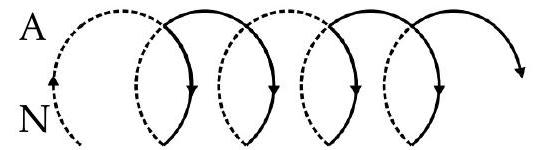
Ans.(i) Line integral of magnetic field over a closed loop is equal to the
Alternatively :
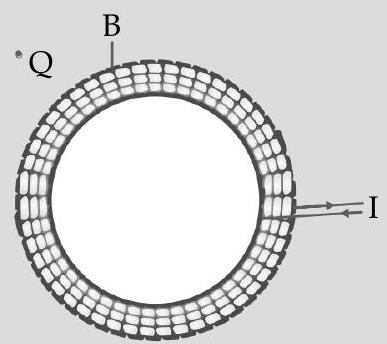
(a)
(b)
Let the current flowing through each turn of the toroid be
Applying Ampere’s circuital law, for the Amperian loop, for interior points.
(ii)
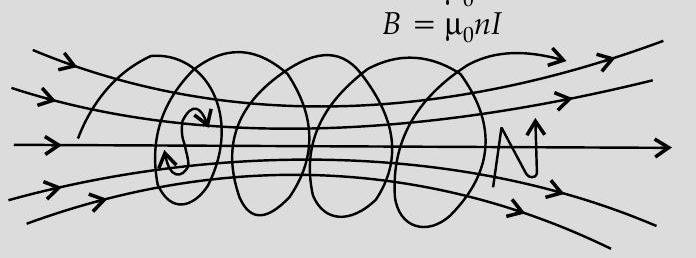
The solenoid contains
The magnetic moments of all loops are aligned along the same direction. Hence, net magnetic moment equals to NIA.
Ans. (i) Ampere’s circuital law deters that the cloned-losp intigral of the
 the current passing through the loop.
the current passing through the loop.

Total incoming current
For loop II,
Applying ampere’s circuital law.


The magnetic files lines will be, as shown
heme end B is Noria end
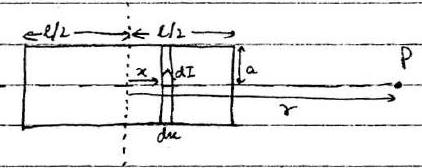
Consider a solenoid as shown Now tate an elementary lop of width che.
for this loop, yield at
then cement in each torn = I.
then
of no. of turn per vent length =n
current in pathourn = cement in each torn =
then no. of torn per unit length
cement is each torn
for a bar magnet.
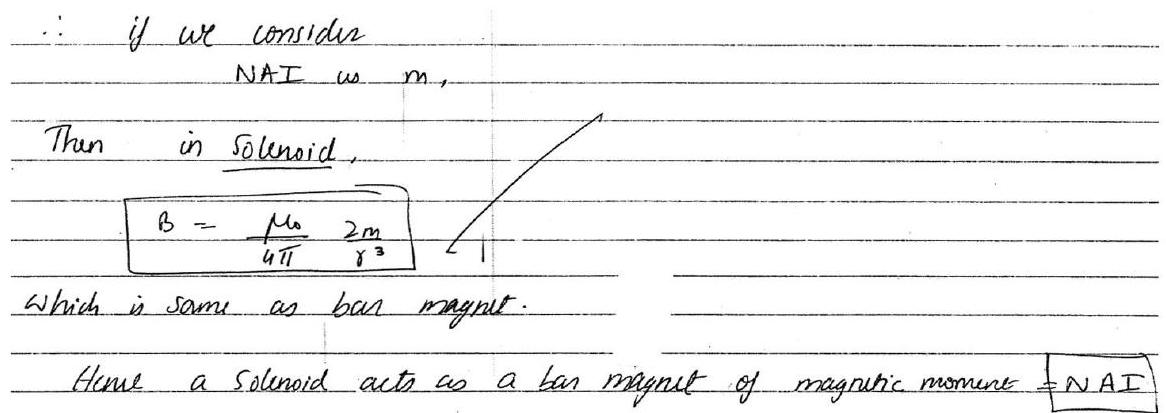
[Topper’s Answer 2015]






