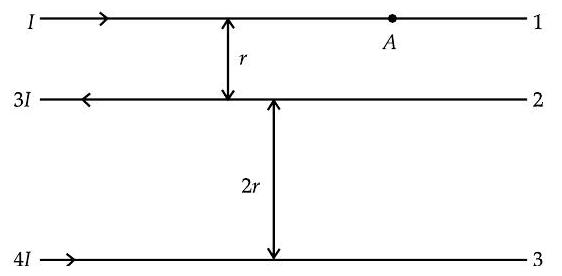
Question: Q. 10. The figure shows three infinitely long straight parallel current carrying conductors. Find the
(i) magnitude and direction of the net magnetic field at point lying on conductor 1 ,
(ii) magnetic force on conductor 2.
U] [Foreign I, II, III, 2017]
Show Answer
Solution:
Ans. (i) Magnitude of magnetic field at
1
Direction of magnetic field at
(ii) Magnitude of magnetic force on conductor
Direction of magnitude force on conductor
(i) into the plane of the paper
out of the plane of the paper/
into the paper
into the paper
(ii) away from wire 1 (towards 3 )
away from 3 (towards 1 )
towards wire 1
towards wire 1
3
[CBSE Marking Scheme 2017]
[I] Q. 11. Two long straight parallel conductors carry steady current and separated by a distance . If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other. Obtain the expression for this force. Hence define one ampere. A [Delhi I, II, III 2015]
Ans. Force experienced by wire ’ ’ of length ’ ’ due to magnetic field of wire ’ ‘.
Force experienced by wire ’ ’ of length ’ ’ due to magnetic field of wire ’ ‘.
Magnetic field due to wire ’ ‘.
Magnetic field due to wire ’ ‘.
since
Similarly,
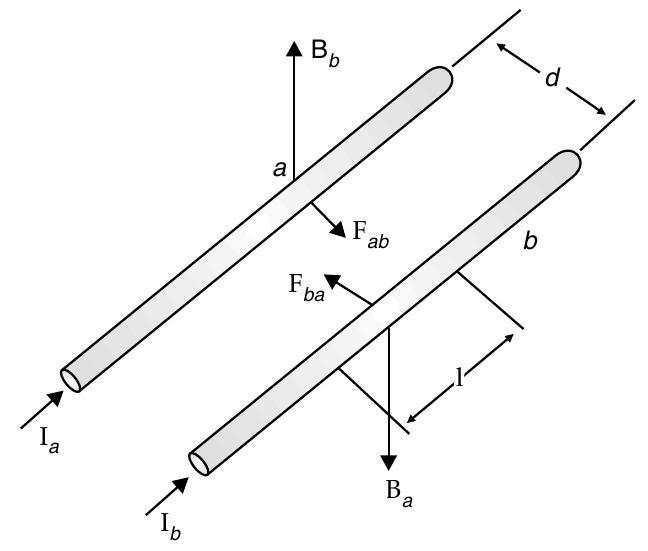
The direction of force experienced by the wire ’ ’ is toward the wire ’ ‘. (As shown in the diagram). Similarly the direction of force experienced by the wire ’ ’ is toward the wire ’ ‘. Thus, the force is attractive.
If two long wires are placed in vacuum at a separation of , one Ampere would be defined as the current in each wire that would produce a force of per unit length of wire.








