Question: Q. 7. (i) How is a toroid different from a solenoid ?
(ii) Use Ampere’s circuital law to obtain the magnetic field inside a toroid.
(iii) Show that in an ideal toroid, the magnetic field (a) inside the toroid and (b) outside the toroid at any point in the open space is zero.
U] [O.D. Comptt. I, II, III 2014]
Show Answer
Solution:
Ans. (i) A toroid can be viewed as a solenoid which has been bent into a circular shape to close on itself. 1 (ii)
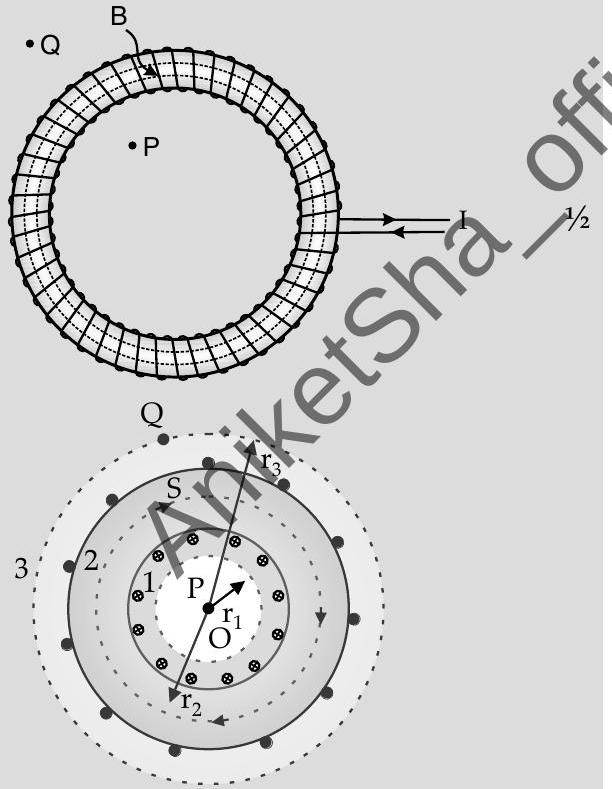
For the magnetic field at a point $\mathrm{S}$ inside a toroid we have
$$ \begin{aligned} B(2 \pi r) & =\mu_{0} N I \ B & =\mu_{0} \frac{N I}{2 \pi r}=\mu_{0} n I \end{aligned} $$
( $n=$ no. of turns per unit length of solenoid) $1 / 2$
$$ n=\frac{N}{2 \pi r} $$
(iii) For the loop 1, Ampere’s circuital law gives $B_{1} .2 \pi r_{1}=\mu_{0}(0)$, i.e. $B_{1}=0$
Thus the magnetic field, in the open space inside the toroid is zero
Also at point $Q$, we have $B_{3}\left(2 \pi r_{3}\right)=\mu_{0}\left(I_{\text {enclosed }}\right)$ But from the section cut, we see that the current coming out of the plane of the paper, is cancelled exactly by the current going into it.
Hence,
$$ I_{\text {enclosed }}=0 $$
$B_{3}=0$
$1 / 2$
[CBSE Marking Scheme 2014]
Answering Tips
- Practice the derivation of Ampere’s Circuital Law to obtain the magnetic field inside a toroid.
