Solution:

Ans. (i) For directions of $\vec{E}, \vec{B}, \vec{v}$

(ii) For magnitudes of $\vec{E}, \vec{B}, \vec{v}$

(i) The velocity $\vec{v}$ of the charged particles, and the $\vec{E}$ and $\vec{B}$ vectors, should be mutually perpendicular. $1 / 2$ Also the forces on $q$, due to $\vec{E}$ and $\vec{B}$ must be oppositely directed. (Also accept if the student draws a diagram to show the directions.)

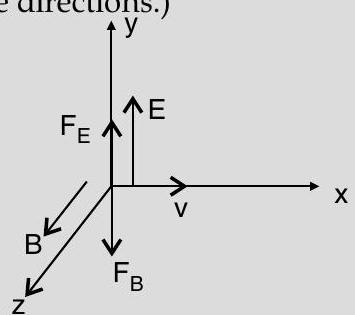
(ii) $q E=q v B$

$1 / 2$

$v=\frac{E}{B}$

$1 / 2$

[Alternatively, The student may write :

Force due to electric field $=q \vec{E}$

Force due to magnetic field $=q(\vec{v} \times \vec{B})$

The required condition is

$$ \begin{align*} q \vec{E} & =-q(\vec{v} \times \vec{B}) \ {[\text { or } \vec{E}} & =-(\vec{v} \times \vec{B})=(\vec{B} \times \vec{v})] \end{align*} $$

(Note : Award 1 mark only if the student just writes :

“The forces, on the charged particle, due to the electric and magnetic fields, must be equal and opposite to each other”)

[CBSE Marking Scheme 2017]

Detailed Answer :

If a charged particle travels in crossed electric and magnetic field, then both fields are perpendicular to each other.

Force on the particle will be :

$$ \begin{aligned} & \vec{F}=\overrightarrow{F_{E}}+\overrightarrow{F_{B}} \ & \vec{F}=\overrightarrow{q E}+q(\vec{v} \times \vec{B}) \end{aligned} $$

As $F_{B}$ is $180^{\circ}$ to $F_{E}$, so

$$ \begin{aligned} & \vec{F}=\overrightarrow{q E}-q(\vec{v} \times \vec{B}) \ & \vec{F}=q\left(E-v_{v} B\right) \hat{j} \end{aligned} $$

Now to select a particle, making resultant force as zero, hence

Now,

$$ 0=q(E-v B) \hat{j} $$

Hence,

$$ \begin{aligned} E-v B & =0 \ E & =v B \end{aligned} $$

Hence,

$$ v=\frac{E}{B} $$