Question: Q. 6. Using Biot-Savart’s law, deduce the expression for the magnetic field at a point
U] [Foreign I, II 2017]
Show Answer
Solution:
Ans. Try yourself, Similar to Q. 3 (b) of Short Answer.
[AI Q. 7. (i) Write the expression for the magnetic force acting on a charged particle moving with velocity
(ii) A neutron, an electron and an alpha particle moving with equal velocities, enter a uniform magnetic field going into the plane of the paper as shown. Trace their paths in the field and justify your answer.

U [Dehhi, II, III 2016]
Ans.
(i)
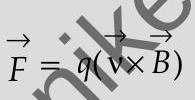
(Give Full credit of this part even if a student writes :
and force
(ii)
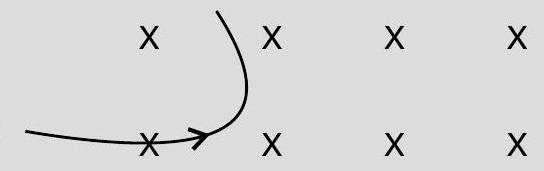
n
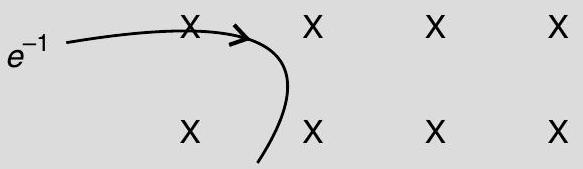
Justification : Direction of force experienced by the particle will be according to the Fleming’s left hand rule/(any other alternative correct rule.) 1/2
[CBSE Marking Scheme 2016]
Detailed Answer :
(i) A charged particle with charge
where,
Here direction of force is shown by cross product of
(ii) velocity and
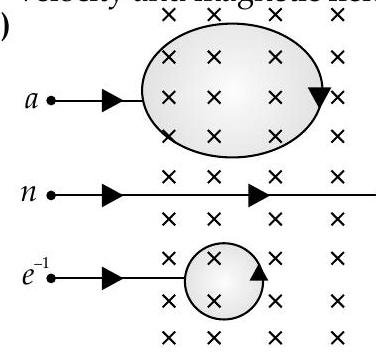
Here,
Neutron will pass without any deviation, as magnetic field, exerts no force on neutral particle.
It is further observed that the direction of force experienced by the particle will be as per Fleming’s left hand rule.






