Question: Q. 3. A bar magnet of magnetic moment
Show Answer
Solution:
Ans. (a) Formula and
Calculation of work done in the two cases
(b) Calculation of torque in case (ii)
(a) Work done
(i)
(ii)
[Also accept calculations done through changes in potential energy.]
(b)
For
We have
[If the student straight away writes that the torque is zero since magnetic moment and magnetic field are anti parallel in this orientation, award full marks]
[CBSE Marking Scheme 2018]
Detailed Answer :
Given,
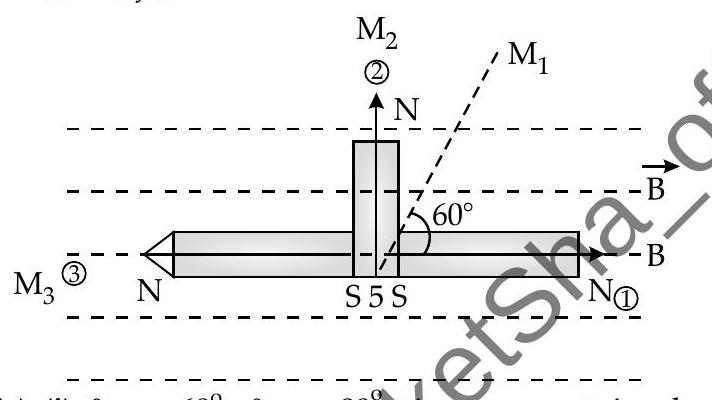
(a) (i)
(ii) Work done in aligning the magnet opposite to magnetic field. i.e.
(b) The Torque on magnet aligned at angle
(i) What is the magnetic moment associated with the solenoid?
(ii) What are the force and torque on the solenoid if a uniform horizontal magnetic field of
U] [CBSE OD Set I, 2015]
Ans. Number of turns in solenoid,
(given)
Area of cross-section of solenoid,
(i) Magnetic moment of the solenoid,
(ii) Net force experienced by the magnetic dipole in the uniformpmagnetic field
Torque on a solenoid,






