Question: Q. 2. Derive the expression for the torque $\tau$ acting on a rectangular current loop of area $A$ placed in a uniform magnetic field $B$. Show that $\vec{\tau}=\vec{m} \times \vec{B}$ where $\vec{m}$ is the magnetic moment of the current loop given by $\vec{m}=I \vec{A}$.
] [Foreign, 2016]
Show Answer
Solution:
Ans. The force, on a wire of length $l$, carrying a current $I$, in a magnetic field $\vec{B}$, is given by $\vec{F}=I l B \sin \theta$ $=I \vec{l} \times \vec{B}$
For a rectangular loop, placed as shown, in a magnetic field $\vec{B}$,
$\mid$ Force on $\operatorname{arm} B C|=|$ Force on $\operatorname{arm} D A \mid=I l B \sin \theta$ where, $\theta=$ angle between side $B C$ and $\vec{B} \quad 1 / 2$ These two forces add up to zero as they are collinear (along the axis of the coil) and act in opposite directions.
$1 / 2$
$\mid$ Force on $\operatorname{arm} A B|=|$ Force on $\operatorname{arm} C D \mid=I b B \sin \theta$
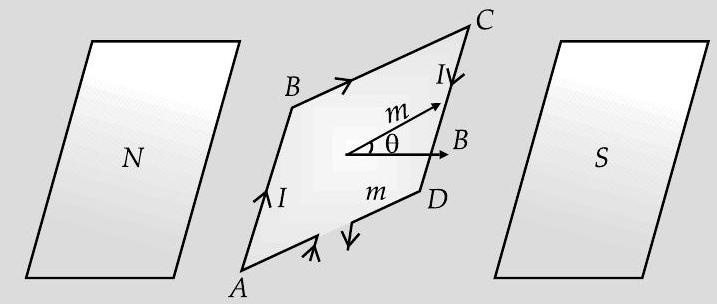
These two equal and opposite forces are not collinear. The perpendicular distance between their lines of action is, as shown,
$$ 2 x \frac{a}{2} \sin \theta=a \sin \theta $$
$\therefore$ Torque acting on the coil, has a magnitude $\tau$,
$\tau=(l b B) \times(a \sin \theta)=I A B \sin \theta(A=a b=$ area of
the coil)
In vector form,
$$ \begin{align*} \vec{\tau} & =I \vec{A} \times \vec{B} \ \overrightarrow{\mathrm{A}} & =\vec{m}, \text { as given } \ \vec{\tau} & =\vec{m} \times \vec{B} \end{align*} $$
[Note : Award these 3 marks, as per the given sequence, even if the student does the derivation by taking the coil in the (special) position where its two arms are parallel and the other two arms are perpendicular to the direction of $\vec{B}$ ]
[CBSE Marking Scheme 2016]
