Question: Q. 1. Define the term magnetic moment of a current loop. Derive an expression for the magnetic field at any point along the axis of a solenoid of length
R [Delhi Comptt. II, III 2017]
Show Answer
Solution:
Ans. Definition of magnetic moment Derivation of expression of magnetic field. 2 Magnetic moment of a current loop is equal to the product of current flowing in the loop and its area and its direction is along area vector as per the right handed screw rule.
Alternatively,
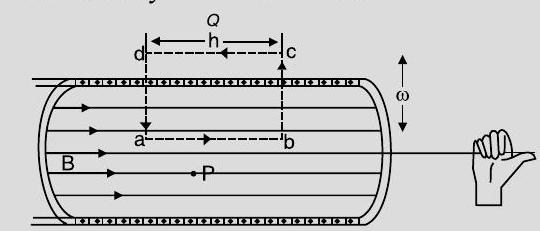
Using Ampere’s circuital law
Commonly Made Error
- Students get confused during deriving the magnetic field in solenoid.
Answering Tip
- Always go step by step during derivation.
Detailed Answer :
Magnetic moment
Bar Magnet as an Equivalent Solenoid :
The magnetic field lines for a bar magnet and a current carrying solenoid resemble very closely.
Therefore, a bar magnet can be thought as a large number of circulating currents in analogy with a solenoid.
Cutting a bar magnet in half is like cutting a solenoid. We get two smaller solenoids with weaker magnetic properties The field lines remain continuous, emerging from one face of the solenoid and entering into other face.
One can test this analogy by moving a small compass needle in the neighborhood of a bar magnet and a current carrying finite solenoid and noting that the deflections of the needle area similar in both the cases.
To prove mathematically that magnetic field produced by a solenoid on any point on the axial line is same as that of a bar magnet. This analogy between bar magnet and solenoid can be shown by calculating the magnetic field at an axial point of solenoid which resemble to that of a bar magnet.
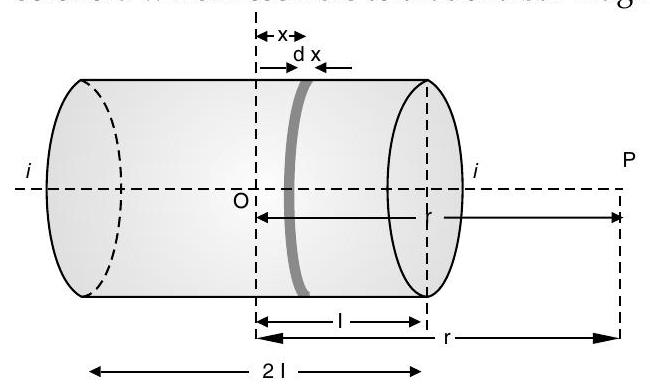
Let
Let
Number of turns in the element
The magnitude of the field at point
If
Total magnetic field at point
$$ \begin{align*} & =\frac{\mu_{0} n i a^{2}}{2 r^{3}}[x]{-l}^{+l}=\frac{\mu{0} n i a^{2}}{2 r^{3}}(2 I) \ & =\frac{\mu_{0}}{4 r} \frac{2 n(2 l) i \pi a^{2}}{r^{3}} \tag{iv} \end{align*} $$
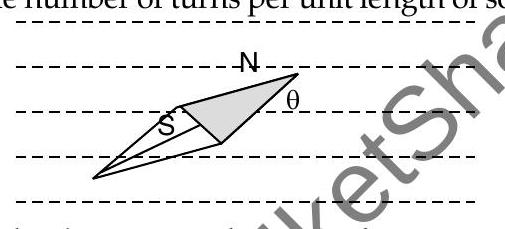
If
This is the expression of magnetic field on the axial line of a short bar magnet.
The magnetic moment of bar magnet is thus equal to the magnetic moment of a equivalent solenoid that produces the same magnetic field.






