Question: Q. 6. (a) An iron ring of relative permeability
(b) Thesusceptibility of a magnetic material is 0.9853 . Identify the type of magnetic material. Draw the modification of the field pattern on keeping a piece of this material in a uniform magnetic field.
R [Delhi & OD, 2018]
Show Answer
Solution:
Ans. (a) Expression for Ampere’s circuital law
Derivation of magnetic field inside the ring
(b) Identification of the material
Drawing the modification of the field pattern
(a) From Ampere’s circuital law, we have,
For the field inside the ring, we can write
using equation (i)
[Award these
written without giving the derivation]
(b) The material is paramagnetic.
The field pattern gets modified as shown in the figure below.
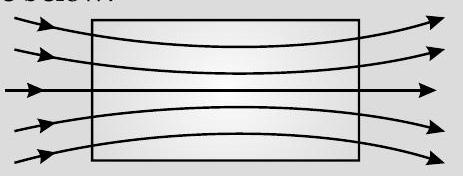
[CBSE Marking Scheme 2018]
Detailed Answer :
(a)
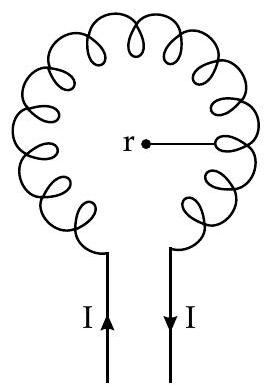
Apply Ampere’s Law for the magnetic field due to iron ring wounded by insulating copper wire, having current I,
or,
or,
or,
But
So,
This is the required expression for magnetic field. Where,
(b) Given : susceptibility
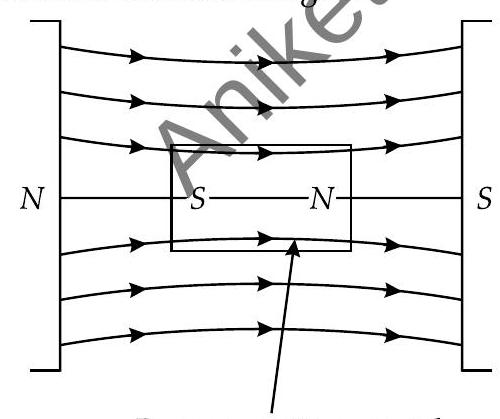
Paramagnetic material






