Solution:

Ans.

(i)

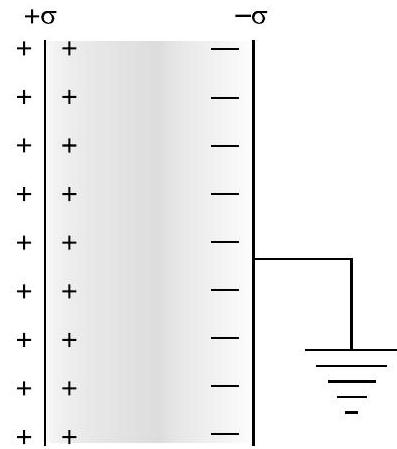
(a) The electric field at point between the plates

$$E=\frac{\sigma }{{\epsilon }_0}$$

and directed from positive plate to negative plate. $\mathbf{1}$

(b) Potential difference $V=E\times$ separation between

$$\therefore \begin{array}{rlr}V& =\frac{\sigma }{{\epsilon }_0}\times dV& =\frac{\sigma }{{\epsilon }_0}d\end{array}$$

(c) Charge on capacitor $=$ magnitude of charge on any of two plates

$$\begin{array}{r}q=\sigma A\text{ and potential difference, }\end{array}$$

$$\begin{array}{}\text{(1)}& V& =\frac{\sigma d}{{\epsilon }_0}\therefore \text{ Capacitance, }C& =\frac{q}{V}=\frac{\sigma A}{\left(\frac{\sigma d}{{\epsilon }_0}\right)}C& =\frac{{\epsilon }_{0}A}{d}\end{array}$$

(ii) When two charged conducting metallic spheres are connected with a conducting wire, then charge flows between the two, till their potentials become equal or redistribution of charges takes place i.e., charge is divided on both the spheres.

AI Q. 6. A capacitor of capacitance $C_1$ is charged to a potential $V_1$ while another capacitor of capacitance $C_2$ is charged to a potential difference $V_2$. The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other.

(i) Find the total energy stored in the two capacitors before they are connected.

(ii) Find the total energy stored in the parallel combination of the two capacitors.

(iii) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.

R [Comptt. Delhi/O.D. I, II, III 2018]

Ans. (i) Finding the total energy before the capacitors are connected

1

(ii) Finding the total energy in the parallel combination

(iii) Reason for difference

(i) We have

Energy stored in a capacitor $=\frac{1}{2}{\mathrm{CV}}^2$

$\therefore$ Energy stored in the charged capacitors

$$ \begin{array}{ll} \mathrm{E}{1} & =\frac{1}{2} C{1} V_{1}^{2} \ \text { And } \quad \mathrm{E}{2} & =\frac{1}{2} C{2} V_{2}^{2} \end{array} $$

$\therefore$ Total energy stored $=\frac{1}{2}{C}_1{V}_1^2+\frac{1}{2}{C}_2{V}_2^2$

$1/2$

(b) Let $\mathrm{V}$ be the potential difference across the parallel combination.

Equivalent capacitance $=(C_1+C_2)$ $1/2$

$$\text{ llel }$$

$1/2$ Since charge is a conserved quantity, we have

$$ \begin{array}{rlr} \left(\mathrm{C}{1}+\mathrm{C}{2}\right) \mathrm{V} & =\mathrm{C}{1} \mathrm{~V}{1}+\mathrm{C}{2} \mathrm{~V}{2} & 1 / 2 \ \Rightarrow \quad \mathrm{V} & =\left[\frac{\mathrm{C}{1} \mathrm{~V}{1}+\mathrm{C}{2} \mathrm{~V}{2}}{\left(\mathrm{C}{1}+\mathrm{C}{2}\right)}\right] & \mathbf{1} \end{array} $$

$\therefore$ Total energy stored in the parallel combination

$$\begin{array}{rlr}& =\frac{1}{2}(C_1+C_2)V^2& =\frac{1}{2}\frac{{(C_1{V}_1+C_2{V}_2)}^2}{(C_1+C_2)}\end{array}$$

(c) The total energy of the parallel combination is different (less) from the total energy before the capacitors are connected. This is because some energy gets used up due to the movement of charges.

[CBSE Marking Scheme, 2018]

UNIT - II