Question: Q. 3. (i) Explain, using suitable diagrams, the difference in the behaviour of (a) conductor and (b) dielectric in the presence of an external electric field. Define the terms polarization of a dielectric and write its relation with susceptibility.

(ii) A thin metallic spherical shell of radius $R$ carries a charge $Q$ on its surface. A point charge $\frac{\mathcal{Q}}{2}$ is placed at its centre $C$ and another charge $+2Q$ is placed outside the shell at a distance $x$ from the centre as shown in the figure. Find (a) the force on the charge at the centre of shell and at the point $A$, (b) the electric flux through the shell.

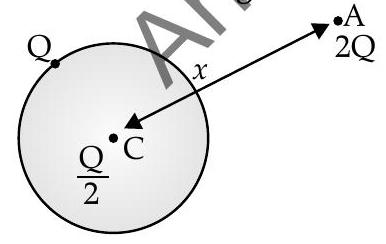
U] [Delhi I, II, III 2015]

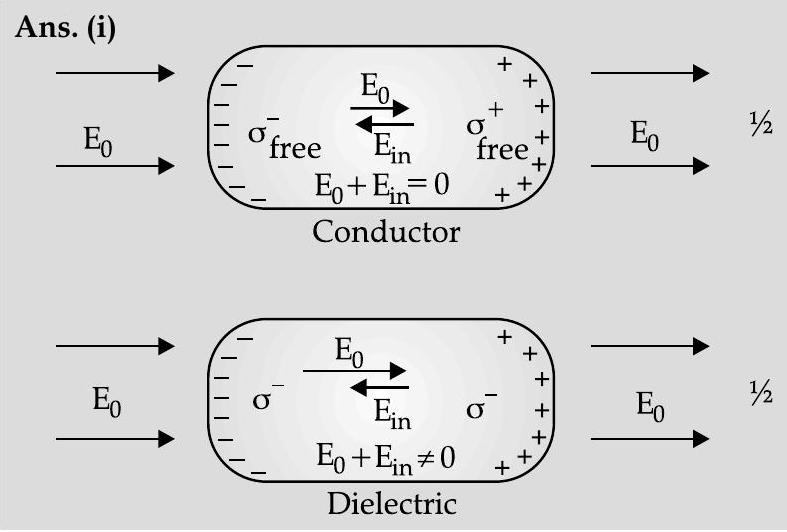
(a) In the presence of electric field, the free charge carriers, in a conductor, move the charge distribution in the conductor re-adjusting itself so that the net electric field within the conductor becomes zero.

$$1/2$$

(b) In a dielectric, the external electric field induces a net dipole moment, by stretching/reorienting the molecules. The electric field, due to this induced dipole moment, opposes, but does not exactly cancel, the external electric field.

$1/2$ Polarisation : Induced dipole moment, per unit volume, is called the polarization. For linear isotropic dielectrics having a susceptibility ${\chi }_C$, we have

$$\begin{array}{}\text{(1)}& P={\chi }_{C}E\end{array}$$

(ii) (a) Net Force on the charge $\frac{Q}{2}$, placed at the centre of the shell, is zero.

1 Force oncharge $2Q$ kept at point $A$

$$F=E\times 2Q$$

$$\begin{array}{rlr}& =\frac{1\left(\frac{3Q}{2}\right)2Q}{4\pi {\epsilon }_0{x}^2}& =\frac{6Q^2}{8\pi {\epsilon }_0{x}^2}=\frac{3Q^2}{4\pi {\epsilon }_0{x}^2}\end{array}$$

OR

$$\frac{(k)3Q^2}{x^2}$$

where, $k=\frac{1}{4\pi {\epsilon }_0}$

(b) Electric flux through the shell

$$\varphi =\frac{Q}{2{\epsilon }_0}$$

$\because$ Charge enclose is $\frac{Q}{2}$

[CBSE Marking Scheme 2015]

AT Q. 4. (i) Compare the individual dipole moment and the specimen dipole moment for $\mathrm{H}{2} \mathrm{O}$moleculeand$\mathrm{O}{2}$ molecule when placed in

(a) Absence of external electric field.

(b) Presence of external electric field.

Justify your answer.

(ii) Given two parallel conducting plates of area $A$ and charge densities $+\sigma$ and $-\sigma$. A dielectric slab of constant $\kappa$ and a conducting slab of thickness $d$ each are inserted in between them as shown.

(a) Find the potential difference between the plates.

(b) Plot $E$ versus $x$ graph, taking $x=0$ at positive plate and $x=5d$ at negative plate.

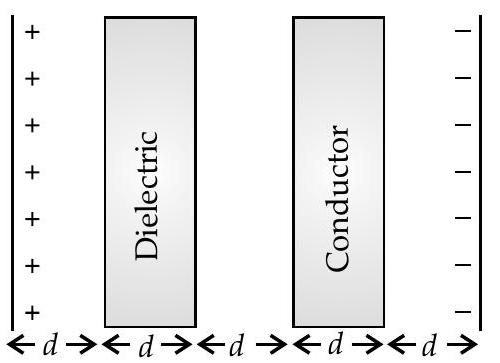
U[CBSE SQP 2015-16]