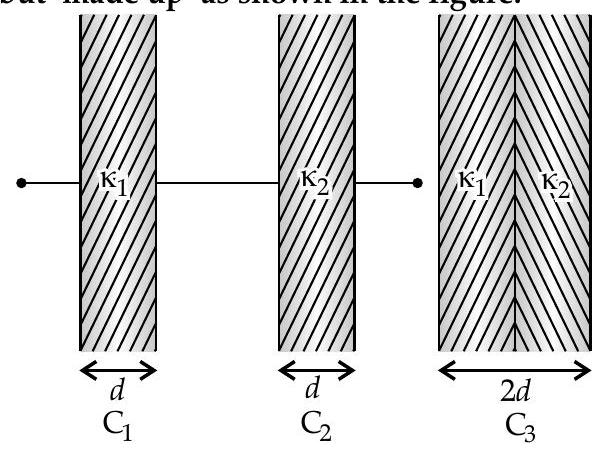
Question: Q. 25. The capacitors
Show Answer
Solution:
Ans. We have
U] [CBSE SQP 2013]
Now, capacitor $\mathrm{C}{3}
$$ \begin{aligned} & \text { We have } \quad C_{1}{ }^{\prime}=\frac{A \varepsilon_{0} \kappa_{1}}{d} \ & \text { and } \quad C_{2}{ }^{\prime}=\frac{A \varepsilon_{0} K_{2}}{d} \ & \Rightarrow \quad C_{3}=\frac{\mathrm{C}{1}{ }^{\prime} \mathrm{C}{2}^{\prime}}{\mathrm{C}{1}{ }^{\prime}+\mathrm{C}{2}{ }^{\prime}}=\frac{A \varepsilon_{0}}{d}\left(\frac{\kappa_{1} \kappa_{2}}{\kappa_{1}+\kappa_{2}}\right) \end{aligned} $$
Hence, the net capacitance of the combination is equal to that of






