Question: Q. 21. (i) Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
(ii) The electric field inside a parallel plate capacitor is E. Find the amount of work done in moving a charge
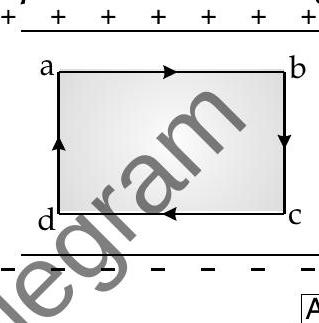
A [Delhi I, II, III 2014]
Show Answer
Solution:
Ans. (i) Work done by the source of potential, in storing
an additional charge
But
Total work done in storing the charge
This work is stored as electrostatic energy in the capacitor.
Energy stored per unit volume
(ii) Work done in moving the charge
Work done from
[CBSE Marking Scheme 2014]
(AI Q. 22. (i) Derive the expression for the capacitance of a parallel plate capacitor having plate area
(ii) Two charged spherical conductors of radii
Ans. (i)

(iii)
Ans. (i)
[CBSE Marking Scheme 2014]
[A] Q. 24. A capacitor of unknown capacitance is connected across a battery of
Calculate :
(i) The potential
Surface
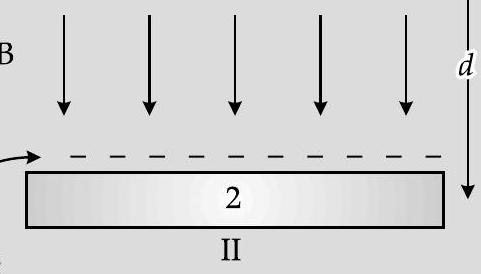
charge density
Electric field between the plates of capacitor
i) When the two charged spherical conductors/are connected by a conducting wire, they acquire the same potential.
i.e.,
Hence, ratio of surface charge densities,
[CBSE Marking Scheme, 2014]






