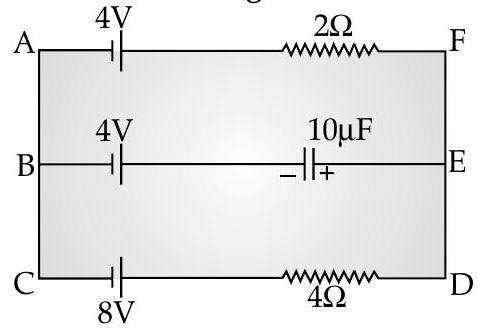
Question: Q. 9. In the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
U [Foreign III 2017]
Show Answer
Solution:
Ans. Value of current
Value of voltage
Value of charge
Try yourself, Similar to Q. 7 Short Answer Type II
[CBSE Marking Scheme 2017]
[AI Q. 10. (i) Find equivalent capacitance between $A$ and $B$ in the combination given below. Each capacitor is of $2 \mu \mathrm{F}$ capacitance.
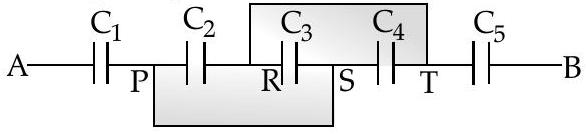
(ii) If a $\mathrm{DC}$ source of $7 \mathrm{~V}$ is connected across $A B$, how much charge is drawn from the source and what is the energy stored in the network ? U[Delhi I 2017]
Ans. (i) Calculation of equivalent capacitance 1
(ii) Calculation of charge and energy stored 1+1
(i) Capacitors $C_{2}, C_{3}$, and $C_{4}$ are in parallel
$\therefore \quad C_{234}=C_{2}+C_{3}+C_{4}$
$\therefore \quad C_{234}=6 \mu \mathrm{F}$
Capacitors $C_{1}, C_{234}$, and $C_{5}$ are in series
$$ \begin{aligned} \frac{1}{C_{\text {eq }}} & =\frac{1}{C_{1}}+\frac{1}{C_{234}}+\frac{1}{C_{5}} \ & =\frac{1}{2}+\frac{1}{6}+\frac{1}{2}=\frac{7}{6} \mu F \ C_{\text {eq }} & =\frac{6}{7} \mu F \end{aligned} $$
(ii) Charge drawn from the source
$$ \begin{aligned} Q & =C_{e q} V \ & =\frac{6}{7} \times 7 \mu C=6 \mu C \end{aligned} $$
Energy stored, $U=\frac{Q^{2}}{2 C_{e q}}$
$$ =\frac{6 \times 6 \times 10^{-12} \times 7}{2 \times 6 \times 10^{-6}} \mathrm{~J} $$
$$ =21 \mu \mathrm{J} $$
