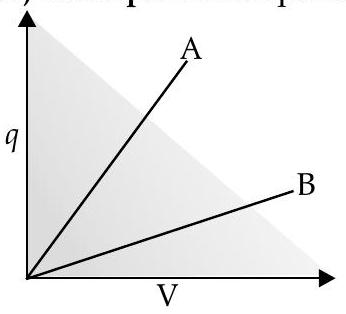
Question: Q. 6. The given graph shows variation of charge versus potential difference for two capacitors and . Both the capacitors have same plate separation but plate area of is greater than that of . Which line ( or ) corresponds to and why?
[Comptt. O.D. I, II, III 2014]
Show Answer
Solution:
Ans. For
Line
1
Since slope of Line is lesser than that of Line .
[CBSE Marking Scheme 2014] 1
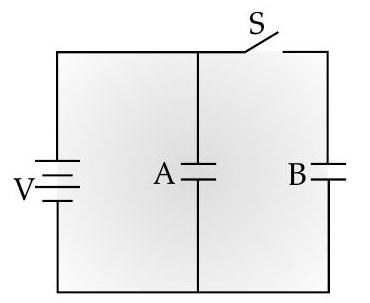
(AI Q. 1. Two identical parallel plate capacitors and are connected to a battery of volts with the switch closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
U [O.D. I, II, III 2017]
Ans. Formula for energy stored Energy stored before
Energy stored after
Ratio
Net capacitance with switch closed
After the switch is opened, capacitance of each capacitor
Energy stored in capacitor
For capacitor ,
[CBSE Marking Scheme 2017]








