Solution:

Ans. (i) Derivation of expression for electric potential due to electric dipole on axial line

(ii) Depiction of equipotential surfaces due to an electric dipole

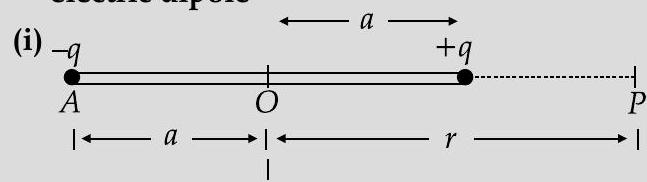
Potential due to charge $-q$ at $A$ :

$$ V_{A}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{-q}{(r+a)} $$

Potential due to charge $+q$ at $B$ :

$$ V_{B}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{(r-a)} $$

Potential at point $P, V=V_{A}+V_{B}$

Net potential at point $P$ :

$V=\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{-1}{(r+a)}+\frac{1}{(r-a)}\right]$

$1 / 2$

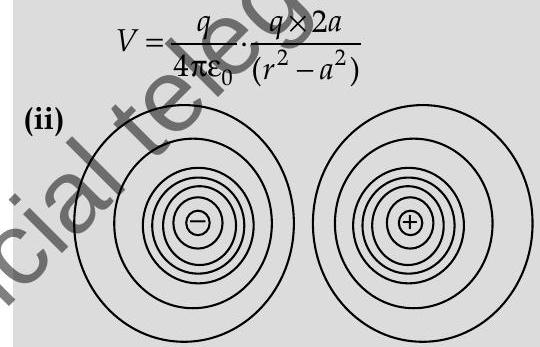
[CBSE Marking Scheme 2017]

AI Q. 3. Define an equipotential surface. Draw equipotential surfaces :

(i) in the case of a single point charge and

(ii) in a constant electric field in $z$-direction.

Why the equipotential surfaces about a single charge are not equidistant?

(iii) Can electric field exist tangential to an equipotential surface? Give reason.

R [O.D. I, II, III 2016]

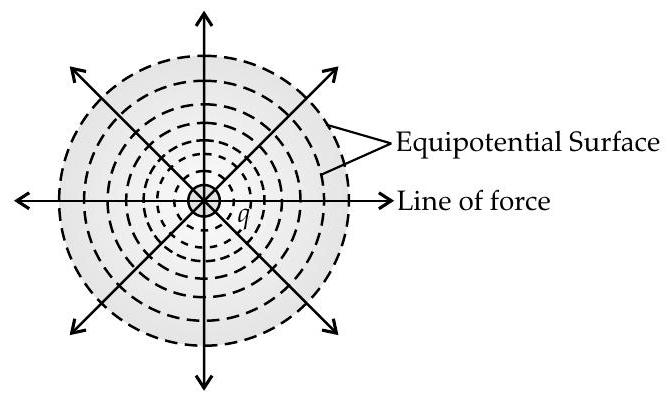
Ans. Equipotential surface is a surface which has equal potential at every point on it.

(i) Equipotential surfaces due to single point charge are concentric spheres having charge at the centre.

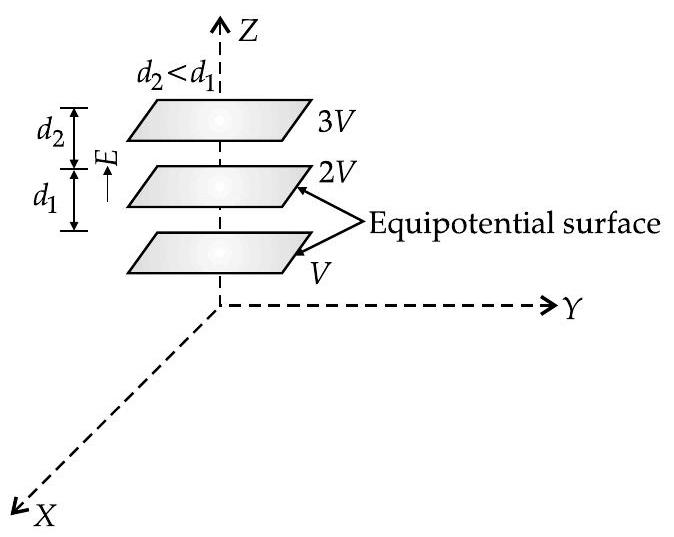
(ii) In constant electric field along $z$-direction, the perpendicular distance between equipotential surfaces remains same.

For single charge, equipotential surface will be series of concentric spherical shells with charge at centre,

$$ d r \propto \frac{1}{E} $$

the separation $d r$ between equipotential surfaces will go on increasing with decrease in electric field.

(iii) No, because if the surface is not equipotential then it would mean that there is tangential component of electric field along surface.

This component will result in motion of electrons, but since we have static fields, this is not possible. 1