Question: Q. 6. Two closely spaced equipotential surfaces
U] [Delhi Comptt. I, II, III 2014]
Show Answer
Solution:
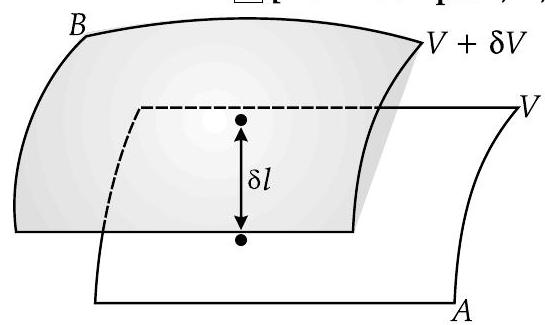
Ans. Work done in moving a unit positive charge along distance
$$ \begin{aligned} \left|\mathrm{E}{l}\right| \delta l & =V{A}-V_{B} \ & =V-(V+\delta V)=-\delta V \end{aligned} $$
(i) Electric field is in the direction in which the potential decreases the steepest.
(ii) The magnitude of electric field is given by the change in the magnitude of potential per unit displacement, normal to the equipotential surface at the point.
[CBSE Marking Scheme 2014] 1/2






