Question: Q. 4. test charge is moved without acceleration from to along the path from to and then from to in electric field as shown in the figure.
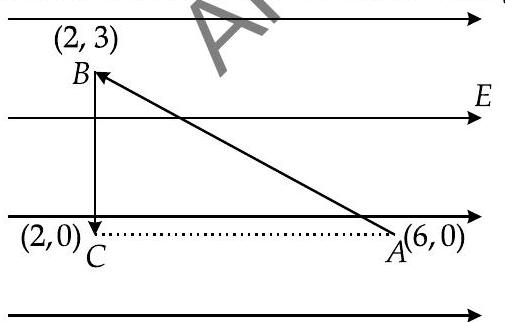
(i) Calculate the potential difference between and C.
(ii) At which point (of the two) is the electric potential more and why?
A [O.D. I, II, III 2012]
Show Answer
Solution:
Ans. Since,
Therefore,
At point , potential is more
etric field is in the direction in which the potential decreases.
[CBSE Marking Scheme 2012]
Detailed Answer :
(i) From the figure, as work done is independent of path, so moving a charge from point to and further from point to , we will take a direct path from point to . So potential difference between points and is given as :
As direction of test charge ’ ’ is opposite to direction of electric field along , so angle between and will be , hence we can write this as :
(ii) As direction of electric field is high to low potential, so
Also, with as positive Potentialincreases when charge is moved against the direction of electric field, so potential will be more at point .







