Question: Q. 12. The currents flowing in the two coils of selfinductance
A [Foreign 2014]
Show Answer
Solution:
Ans. (i) Induced emf (voltage) in a coil,
(ii) Power supplied
As power is same for both coils
(iii) Energy stored in a coil,
[CBSE Marking Scheme 2014]
Long Answer Type Questions
[AT] Q. 1. (a) State the principle of an
(b) An aeroplane is flying horizontally from west to east with a velocity of
Ans. (a) Principle of
Derivation of the expression for induced emf
(b) Calculation of potential difference
The
When the magnetic flux through a coil changes, an emf is induced in it.
As the coil rotates in magnetic field the effective area of the loop, (i.e.,
(b) Potential difference developed between the ends of the wings
Given:

Wing span,
Vertical component of Earth’s magnetic field
[CBSE Marking Scheme 2018]
Answering Tips
- While answering the question related to ac generator always remember to make a proper and labelled diagram following with explanation of principle, construction and working of generator.
Detailed Answer :
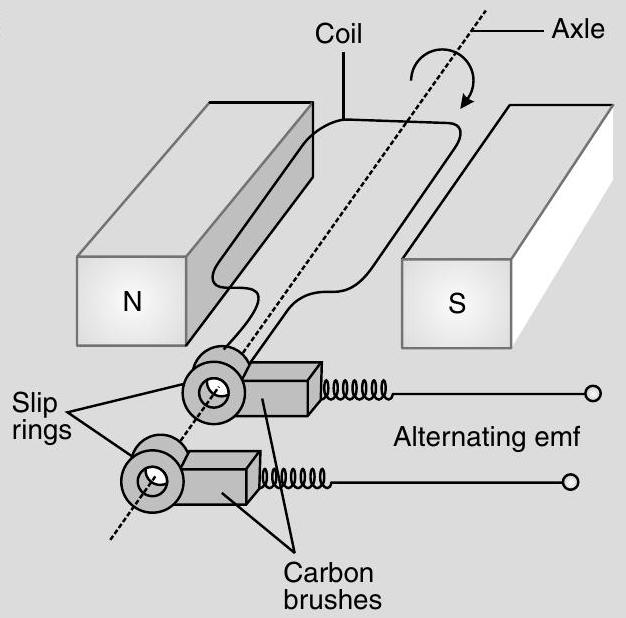
(a) A.C. generator :
A.C. generator is a device which converts mechanical energy into electric energy.
Principle : It works on the principle of electromagnetic induction.
Working : It consists of
(i) Armature coil of large number of turns of copper wire wound over soft iron core soft iron core is used to increase magnetic flux. (ii) Field magnets are used to apply magnetic field in which armature coil is rotated with its axis perpendicular to field lines.
(iii) Slip rings used to provide movable contacts of armature coil with external circuit containing load.
(iv) Brushes are the metallic pieces used to pass an electric current from armature coil to the external circuit containing load.
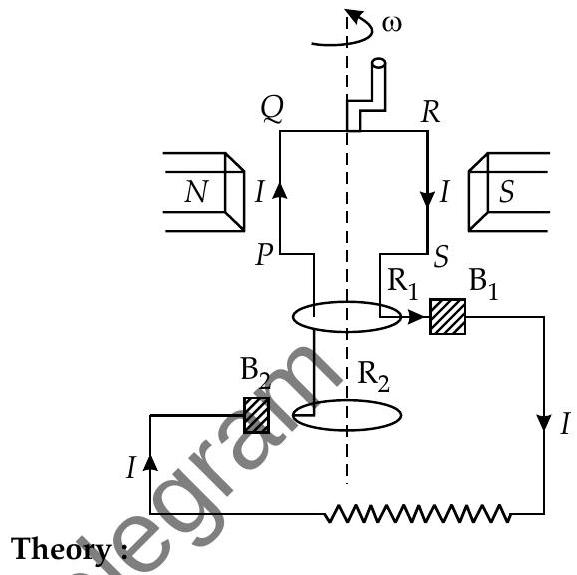
CorSider a coil PQRS free to rotate in a uniform magnetic field
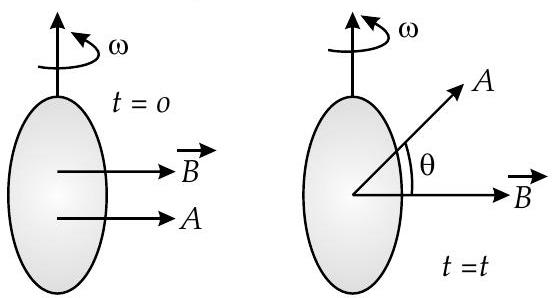
As the coil rotates, the magnetic flux linked with it changes. An induced emf is set up in the coil which is given by,
If the coil has
Thus, the induced emf varies sinusoidally with time ’
We consider the following special cases :
(i) When
(ii) When
(iv) When
(v) When
As the coil continues to rotate in the same sense the same cycle of changes repeats again and again. Such an emf is called sinusoidal or alternating emf. Both the magnitude and direction of this emf changes regularly with time.
- The fact that an induced emf is set up in a coil when rotated a magnetic field forms the basic principle of a dynamo or a generator.
- The electric current produced varies sinusoidally with time, so is known as ‘alternating current’ and hence the generator is known as ‘A.C. generator’ .
(b) As






