Question: Q. 11. Derive the expression for the magnetic energy stored in a solenoid in terms of magnetic field $B$, area $A$ and length $l$ of the solenoid carrying a steady current $I$. How does this magnetic energy per unit volume compare with the electrostatic energy density stored in a parallel plate capacitor?
Show Answer
Solution:
Ans. Rate of work done,
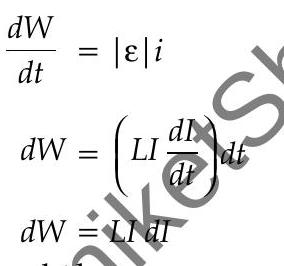
Total amount of work done,
$$ \begin{aligned} \int d W & =\int L I d I \ W & =\frac{1}{2} L I^{2} \end{aligned} $$
For the solenoid :
Inductance, $L=\mu_{0} n^{2} A l$; also $B=\mu_{0} n I$
$$ \begin{aligned} & \therefore \quad W=U_{B}=\frac{1}{2} L I^{2} \ & =\frac{1}{2}\left(\mu_{0} n^{2} A l\right)\left(\frac{B}{\mu_{0} n}\right)^{2} \ & =\frac{B^{2} A l}{2 \mu_{0}} \end{aligned} $$
$1 / 2$
Magnetic energy per unit volume $=\frac{B^{2}}{2 \mu_{0}}$
Also, Electrostatic Energy Stored Per Unit Volume
$$ =\frac{1}{2} \varepsilon_{0} E^{2} $$
