Solution:

Ans. (i) In one revolution

Change of area, $dA=\pi l^2$

$\therefore$ change of magnetic flux

$$\begin{array}{rlr}d\varphi =\overrightarrow{B}\cdot \overrightarrow{dA}& =B\cdot dA\cos 0^{\circ }& =B\pi l^2\end{array}$$

(a) Induced emf, $\epsilon =B\pi l^2/T=B\pi l^{2}v1/2$

(b) Induced current in the rod, $I=\frac{\epsilon }{R}=\frac{\pi \nu B{l}^2}{R}1$

(ii) Force acting on the rod, $F=IlB$

$$=\frac{\pi v{B}^2{l}^3}{R}$$

The external force required to rotate the rod opposes the Lorentz force acting on the rod/ external force acts in the direction opposite the Lorentz force.

(iii) Power required to rotate the rod

$$\begin{array}{rlrl}\text{ Power }& =\text{ Force }\times \text{ velocity }P& =F\times vP& =\frac{\pi v{B}^2{l}^3}{R}\times v\end{array}$$

[CBSE Marking Scheme, 2014]

Detailed Answer :

(i) In a revolution, change in Area $=\pi l^2$

Given, $$ Magnetic field $=B$

$$\begin{array}{llll}\because & d\varphi =\overrightarrow{B}\cdot \overrightarrow{dA}\text{ or }& d\varphi =B\cdot \pi l^2\cos 0^{\circ }\text{ or }& d\varphi =B\pi l^2\end{array}$$

Now, induced emf

$$\text{Multiple tag}$$

(ii)

According to law, the external force acts in the directionopposite toe lorentz force.

Power $=$ Force $\times$ velocity

$$\begin{array}{}\text{(2)}& & =\frac{B^2{l}^3\pi v}{R}\times v& =\frac{\pi v{B}^2{l}^{3}v}{R}\end{array}$$

TOPIC-2

Eddy Currents, Selfand Mutual Induction and AC Generator

Revision Notes

Eddy Currents

• Current loops inducedin moving conductors are called eddy currents. They can create significant drag, called as magnetic damping.

Eddy currents give rise to magnetic fields that oppose any external change in the magnetic field.

Mathematically,

$$i=\frac{e}{R}$$

Eddy currents are induced electric currents that flow in a circular path

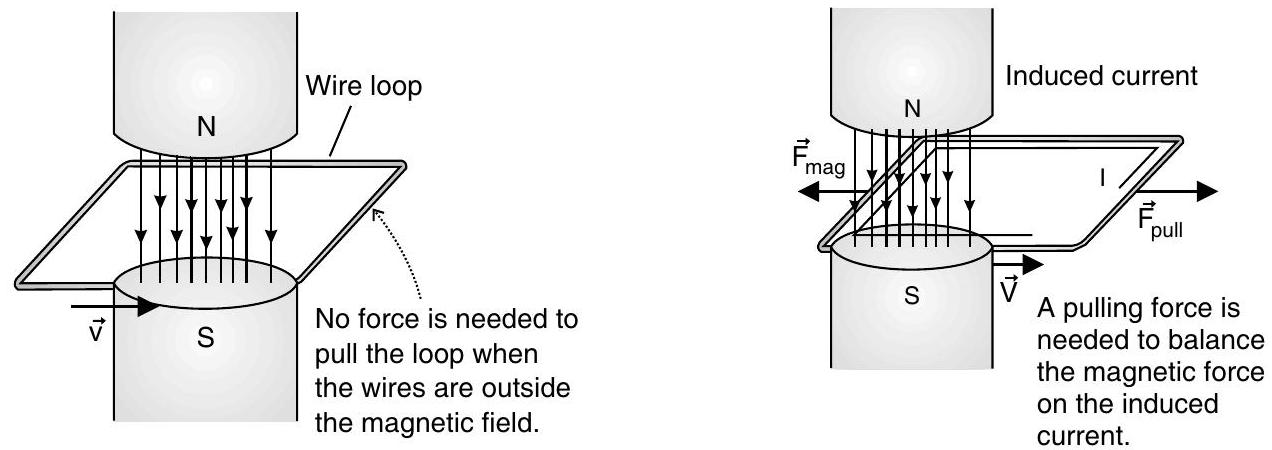
Eddy currents flowing in a material will generate their own secondary magnetic field that opposes the coil’s primary magnetic field.

Mutual Induction

The production of induced emf in a circuit, when the current in the neighbouring circuit changes is called mutual induction.

When the circuit of the primary coil is closed or opened, deflection is produced in the galvanometer of the secondary coil. This is due to the mutual induction.

$>$ The mutual induction between two coils depends on the following factors :

• The number of turns of primary and secondary coils.
• The shape, size or geometry of the two coils. i.e., the area of cross-section and the length of the coils.

Coefficient of mutual induction :

• Suppose, the instantaneous current in the primary coil is $I$. Let the magnetic flux linked with the secondary coil be $\varphi$. It is found that the magnetic flux is proportional to the current. i.e.,

$$\begin{array}{}\text{(i)}& \varphi \propto I\text{ or }\varphi =MI\end{array}$$

where, $M$ is the constant of proportionality. It is called coefficient of mutual induction.

The induced emf $\epsilon$ in the secondary coil is given by

$$\begin{array}{}\text{(ii)}& \epsilon =-\frac{d\varphi }{dt}=-M\frac{dI}{dt}\end{array}$$

The negative sign is in accordance with the Lenz’s law i.e., the induced emf in the secondary coil opposes the variation of current in the primary coil.

From the equation (ii), we find

Therefore,

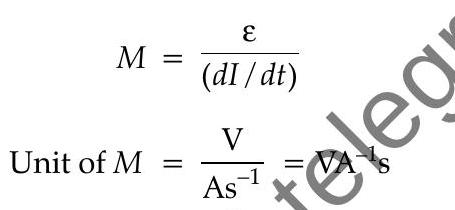
If $n_1,n_2$ be the number of turns in primary and secondary coils permit length and $r$ be their radius, then coefficient of mutual inductance is given as

Self-Induction :

The production of induced emf in a circuit, when the current in the same circuit changes is known as selfinduction.

Suppose the instantaneous current in the circuit Is $I$ and if the magnetic flux linked with the solenoid is $\varphi$, then it is found that :

$$\begin{array}{}\text{(i)}& \varphi \propto 1\text{ or }\varphi =LI\end{array}$$

where, $L$ is the constant of proportionality. It is called coefficient of self-induction.

The induced emf $\epsilon$ in the coil is given by

$$\begin{array}{}\text{(ii)}& \epsilon =-\frac{d\varphi }{dt}=-L\frac{dI}{dt}\end{array}$$

The negative sign is in accordance with the Lenz’s law i.e., the induced emf opposes the variation of current in the coil. From the equation (ii), we find :

$$\begin{array}{}\text{(iii)}& L=\epsilon /(dI/dt)\end{array}$$

Then, the coefficient of self-induction is the ratio of induced emf in the circuit to the rate of change of the current in the circuit.

Unit of $\mathrm{L}:$ The unit of self-induction is also called henry (symbol H). From equation (ii), we find that if

$$\begin{array}{rlr}d\mathrm{I}/dt& =1{\mathrm{AS}}^{-1}\text{ and }\epsilon =1\mathrm{V}L& =1\mathrm{H}\Rightarrow \text{ Unit of }H={\mathrm{VA}}^{-1}\mathrm{s}\end{array}$$

If a rod of length $l$ moves perpendicular to a magnetic field $B$ with a velocity $v$, then the induced emf produced across it, is given by

In general, we have,

$$\begin{array}{rlr}& \epsilon =\overrightarrow{bBl}& \epsilon =\overrightarrow{B}\cdot (\overrightarrow{v}\times \overrightarrow{l})\end{array}$$

If a metallic rod of length $l$ rotates about one of its ends in a plane perpendicular to the magnetic field, then the induced emf produced across its ends is given by

$$\epsilon =\frac{B\omega l^2}{2}=\frac{B2\pi f{l}^2}{2}=BAf$$

Here, $\omega =$ angular velocity of rotation, $A=\pi l^2=$ area of circle and $f=$ frequency of rotation.

Inductance in the electrical circuit is equivalent to the inertia (mass) in mechanics.

• When a bar magnet is dropped into a coil, the electromagnetic induction in the coil opposes its motion, so the magnet falls with acceleration less than that due to gravity.

The inductance of a coil depends on the following factors :

• area of cross-section,
• number of turns
• permeability of the core.

D Unit of induction, $H=\frac{\mathrm{Wb}}{\mathrm{A}}=\frac{\mathrm{Vs}}{\mathrm{A}}=\mathrm{\Omega }$.s

The inductance of a circular coil is given by :

or

$$\begin{array}{rlrl}& L=\frac{\varphi }{I}=\frac{BAN}{I}=\frac{\mu }{4\pi }\cdot \frac{(2\pi NI)}{rI}\times AN& L=\frac{\mu N^2}{2r}A=\frac{\mu N^2}{2r}\times \pi r^2& L=\frac{\mu N^2\pi r}{2}\end{array}$$

The inductance of a solenoid of length $l$ is given by

or

$$\begin{array}{rlrlr}& L=\frac{\varphi }{I}=\frac{BAN}{I}=\left(\frac{\mu NI}{l}\right)\frac{AN}{I}& [\because B=\frac{\mu NI}{l}]& L=\frac{\mu N^{2}A}{l}=\mu n^{2}Al=\mu n^{2}V& [\because n=\frac{N}{l}]\end{array}$$

$$[\because B=\frac{\mu }{4\pi }\cdot \frac{2\pi NI}{r}]$$

Here, $n=N/l=$ number of turns per unit length and $V=\mathrm{A}l=$ volume of the sonoid.

If two coils of inductance $L_1$ and $L_2$ are coupled together, then their mutual inductance is given by

where, $k$ is called the coupling constant.

$$M=k\sqrt{L_1{L}_2}$$

The value of $k$ lies between 0 and 1 .

For perfectly coupled coils, $k=1$, it means that the magnetic fluxytprimary coil is completely linked with the secondary coil.

Eddy currents do not cause sparking.

If a current $I$ is set up in a coil of inductance $L$, then the magnetic field energy stored in it is given by

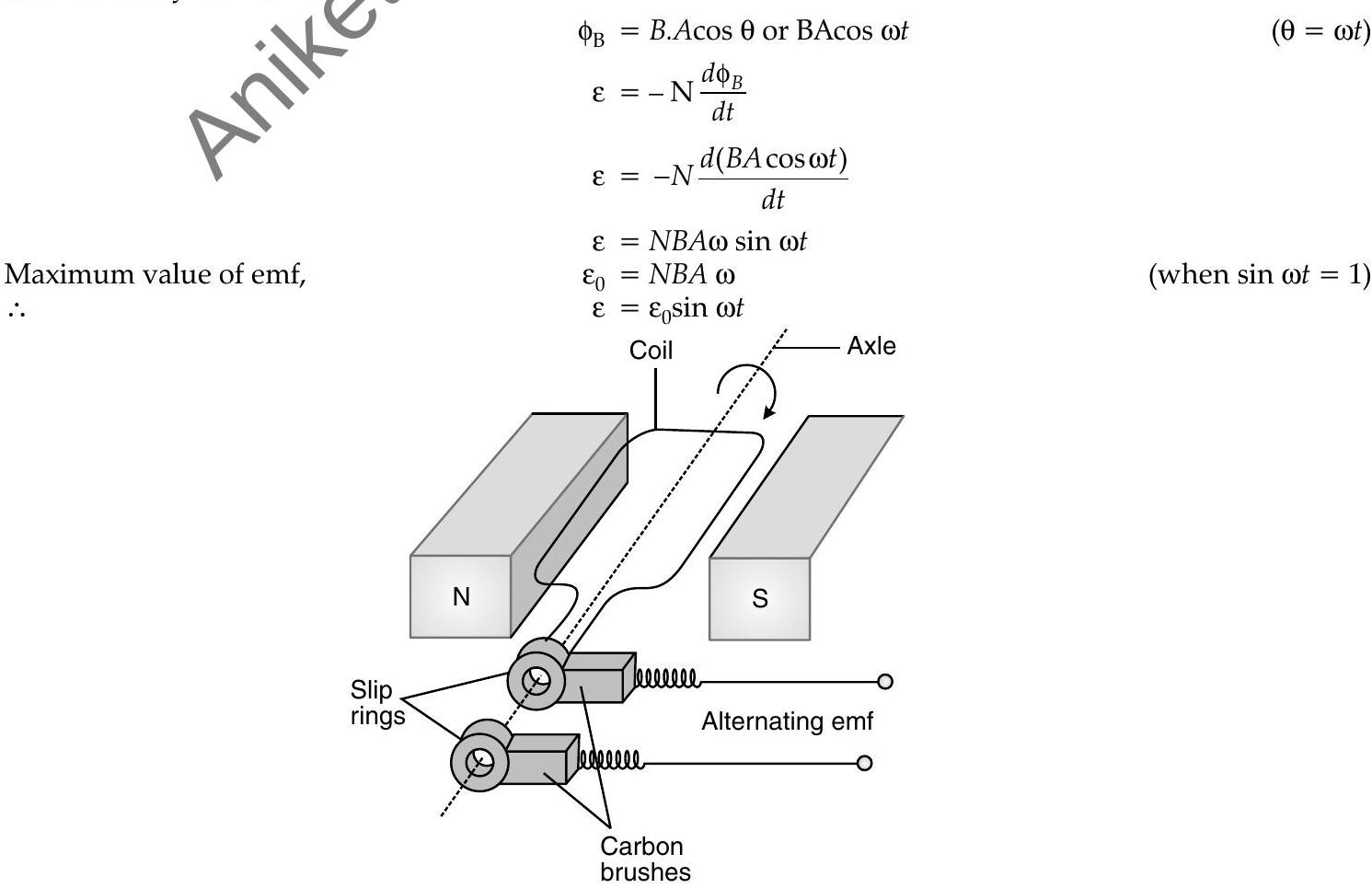
AC Generator

It converts mechanical energy into electrical energy.

• It is based on the principle of mutual induction. It has mainly three components :
• Rotator Coil : It can rotate about an axis on a shaft.
• Stator Coil : It provides magnetic field.
• Commutator : It is pair of slip rings and carbon brushes. It will facilitate flow of current between moving coil and stationary circuit.

Know the Terms

Back emf : emf generated by a running motor due to coil that turns in a magnetic field which opposes the voltage that powers the motor.

• Inductor : It is a device used to store electrical energy in a from of magnetic field when electric current flows.

emf produced by an electric generator : $\epsilon =$ NBA $\omega \sin (\omega \mathrm{t})$

Know the Formulae

$>$ For Self Inductor

$$\begin{array}{rlrlr}\epsilon & =\frac{d\varphi }{dt}=-L\frac{dI}{dt}\epsilon & =\frac{d\varphi }{dt}=-M\frac{dI}{dt}{L}_s& =L_1+L_2+L_3+\dots .\frac{1}{L_p}& =\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}+\dots .\end{array}$$

For Mutual Inductor

The inductance in series is given by

Mutual Inductance of two coils is given by

$$M=\frac{{\mu }_0{\mu }_r{N}_P{N}_S{A}_P}{I_P}=\frac{{\mu }_0{\mu }_r{N}_P{N}_S{A}_S}{I_P}$$

where, ${\mu }_0$ is the permeability of fee space $(4\pi \times {10}^{-7})$

${\mu }_r$ is the relative permeability of the soft iron core

$N_S$ is number of turns is secondary coil.

$N_P$ is number of turns is primary coil.

$A_P$ is the cross-sectional area of primary coil in ${\mathrm{m}}^2$.

$A_S$ is the cross-sectional area of secondary will in ${\mathrm{m}}^2$.

$I$ is the coil current.

$>$ For A.C. Generator $\epsilon ={\epsilon }_0\sin \omega t$ or $\epsilon ={\epsilon }_0\sin 2\pi \nu t$

? Objective Type Question