Question: Q. 4. The magnetic field through a single loop of wire, $12 \mathrm{~cm}$ in radius and $8.5 \Omega$ resistance, changes with time as shown in the figure. The magnetic field is perpendicular to the plane of the loop. Plot induced current as a function of time.
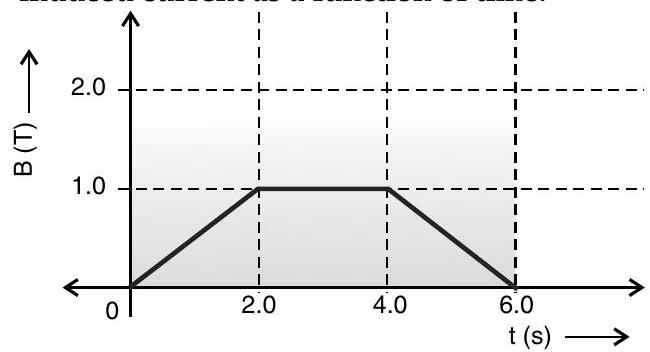
A [CBSE SQP 2015]
Show Answer
Solution:
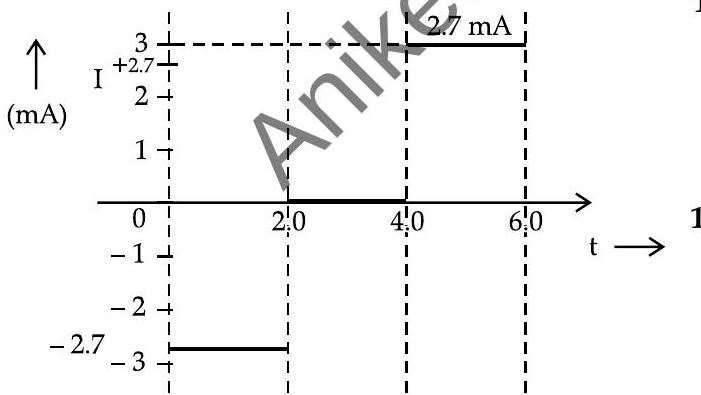
Ans.
$$ \begin{aligned} \varepsilon & =-\frac{d \phi}{d t} \ & =-\pi R^{2} \times \frac{d B}{d t} \ & =-\frac{22}{7} \times(0.12)^{2} \times \frac{1}{2} \ \varepsilon & =-0.023 \mathrm{~V} \ I & =\frac{\varepsilon}{R} \ & =-2.7 \mathrm{~mA} \text { for } 0<t<2 \mathrm{~s} . \end{aligned} $$
Similarly :
| $0<t<2 \mathrm{~s}$ | $2<t<4 \mathrm{~s}$ | $4<t<6 \mathrm{~s}$ | |
|---|---|---|---|
| $\varepsilon(\mathrm{V})$ | -0.023 | 0 | +0.023 |
| $\mathrm{I}(\mathrm{mA})$ | -2.7 | 0 | +2.7 |
[AI Q. 5. A rectangular conductor $L M N O$ is placed in a uniform magnetic field of $0.5 \mathrm{~T}$. The field is directed perpendicular to the plane of the conductor.
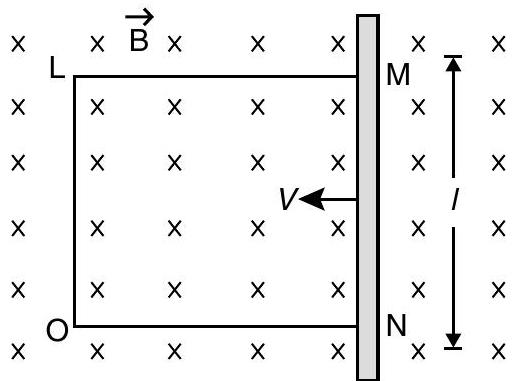
When the arm $M N$ of length of $20 \mathrm{~cm}$ is moved towards left with a velocity of $10 \mathrm{~ms}^{-1}$, calculate the emf induced in the arm. Given the resistance of the arm to be $5 \Omega$ (assuming that other arms are of negligible resistance) find the value of the current in the arm.
A [O.D. I, II, III 2013]
Ans. Let $O N$ be at some point $x$.
The emf induced in the loop $=\varepsilon$
$$ \begin{aligned} \varepsilon & =\frac{-d \phi}{d t}=\frac{-d(\mathrm{~B} l x)}{d t}=B l v \ & =0.5 \times 0.2 \times 10=1 \mathrm{~V} \end{aligned} $$
$\therefore$ Current in the arm,
$$ \begin{equation*} I=\frac{\varepsilon}{R}=\frac{1}{5}=0.2 \mathrm{~A} \tag{1} \end{equation*} $$
